Диаграмма растяжения чугуна и стали

Конспект лекционных и практических занятий по дисциплине «Сопротивление материалов», страница 8

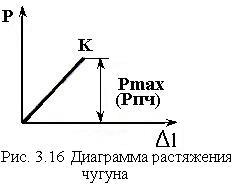Диаграмма растяжения чугуна носит прямолинейный характер, при этом разрыв образца происходит без пластических деформаций (рис. 3.16). По диаграмме растяжения можно определить максимальную нагрузку , по которой определяют единственную характеристику прочности — предел прочности .

в) испытание на сжатие малоуглеродистой стали

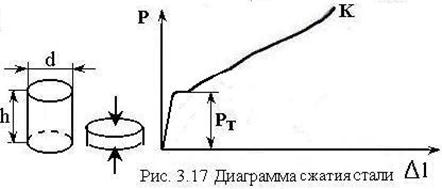Диаграмма сжатия образцов из малоуглеродистой стали (рис. 3.17) похожа на диаграмму растяжения той же стали но при этом точка соответствует не разрыву образца, а прекращению испытаний. При этом образец может быть доведен до сильно сплюснутого состояния, не разрушаясь. Пределы текучести на растяжение и сжатие образцов из одного и того же высокопластичного материала примерно одинаковы:

г) испытание на сжатие чугуна

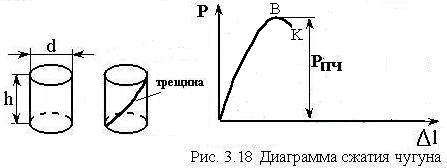Диаграмма сжатия чугуна (рис 3.18) имеет близкий к прямолинейной зависимости характер, при этом разрушение образца происходит с малыми пластическими деформациями с образованием трещины под углом в 45 градусов к линии нагружения (в этой площадке действуют наибольшие касательные напряжения). Предел прочности при сжатии, определяемый по наибольшей нагрузке, значительно больше предела прочности при растяжении: .

3.7 Пример выполнения расчетно-графической работы № 2.1: Осевая деформация стержня переменного сечения

Дано:

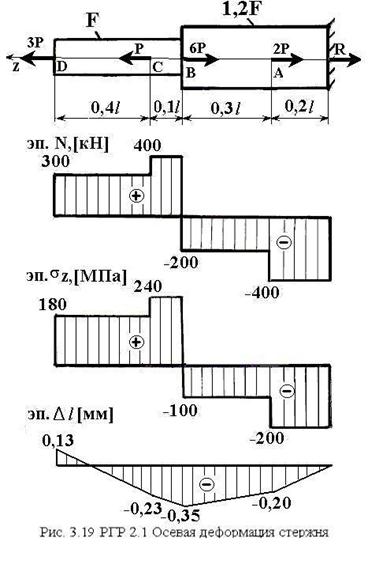
Задание (рис. 3.19):

1) построить эпюру осевых сил N(z)

2) построить эпюру нормальных напряжений

1) определить минимально необходимую площадь поперечного сечения из условия прочности по нормальным напряжениям

4) построить эпюру абсолютных удлинений

Решение.

1) Заменяя жесткую заделку на реакцию , и совмещая начало координат с неподвижным концом стержня, составляем уравнение равновесия всех сил на ось стержня:

(реакция в заделке направлена в противоположную сторону по отношению к показанному на рисунке)

Выражение для осевых сил (для 4-х участков стержня):

.

Символ означает, что слагаемое, следующее за ним, следует учитывать только при превышении осевой координаты указанного значения.

Строим эпюру осевых сил, которая является кусочно-постоянной функцией и меняется скачкообразно в точках приложения сосредоточенных сил.

2) Выражение для осевых сил и нормальных напряжений для каждого из участков в отдельности:

3) Условие прочности при одноосном растяжении-сжатии:

Определяем минимально-необходимую площадь поперечного сечения

3) Определяем значения нормальных напряжений для найденного значения площади сечения:

Строим эпюру нормальных напряжений, которая является постоянной для участков, где отношение осевой силы к площади сечения одинаково.

4) Определяем абсолютные удлинения участков стержня

(следовательно, в целом, стержень удлиняется)

Строим эпюру продольных перемещений, которая является кусочно-линейной функцией.

4. Кручение стержней круглого поперечного сечения

4.1 Деформация кручения

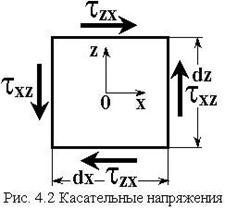
Деформация сдвига определяется изменением первоначально прямого угла между элементами. Данное изменение равно углу сдвига (рис. 4.1).

Чистый сдвиг — напряженно-деформированное состояние, характеризуемое тем, что на гранях элемента возникают только касательные напряжения.

Пусть — абсолютный сдвиг, тогда — относительный сдвиг (угол сдвига)

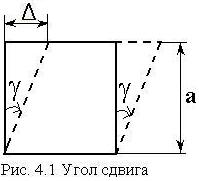
Закон парности касательных напряжений — на взаимно-перпендикулярных площадках касательные напряжения численно равны и направлены так, что стремятся вращать элемент в противоположные стороны.

Составим уравнение равновесия по моментам относительно центра бесконечно-малого элемента единичной толщины выделенного из деформированного тела (рис. 4.2):

,

аналогично .

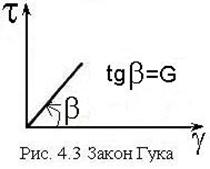
Закон Гука при сдвиге: при малых деформациях касательные напряжения пропорциональны вызываемому ими углу сдвига: , где — модуль упругости материала при сдвиге (модуль сдвига)

Для изотропного материала три упругих константы связаны соотношением: .

Для Ст3: (): .

4.2 Формула для касательных напряжений

Допущения:

— гипотеза плоских сечений: все поперечные сечения, поворачиваясь вокруг оси , остаются плоскими.

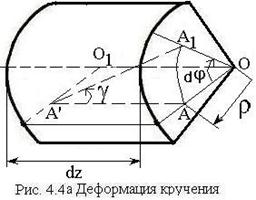— гипотеза прямых радиусов: все радиусы данного сечения остаются прямыми и поворачиваются на один и тот же угол — угол закручивания (см. рис. 4.4а).

На рис. 44а видно, что . Отсюда относительный (погонный) угол закручивания определяется по формуле , а угол сдвига

Суммарный момент от касательных напряжений равен заданному моменту:

и где — жесткость круглого поперечного сечения при кручении.

где — расстояние от центра сечения до произвольной точки.

Условие прочности при кручении: , где — момент сопротивления при кручении.

для сплошного круглого сечения: ,

для полого толстостенного сечения: ,

для тонкостенного кольцевого сечения: .

Правило знаков при кручении: крутящий момент положителен, если при наблюдении со стороны внешней нормали к поперечному сечению, он поворачивает сечение по часовой стрелке (рис. 4.4б).

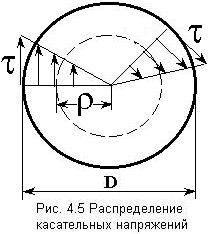
Касательные напряжений при кручении изменяются вдоль радиуса по линейному закону (рис. 4.5): в центре сечения они равны нулю, а наибольших значений достигают на контуре сечения.

Угол закручивания определяется по формуле , где — угол поворота в начале координат. При и : .

Пример.

1) Определить крутящий момент, передаваемый валопроводом корабля на винт, если — мощность двигателя и — частота вращения валопровода известны.

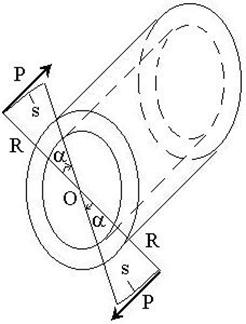2) Определить внутренний и наружный диаметры валопровода из условия прочности по касательным напряжениям при .

Решение:

1) Работа пары сил , создающей крутящий момент равна .

оборотам в минуту соответствует угол, равный рад. Работа в единицу времени определяет мощность двигателя: .

Для : .

2) Из условия прочности определяем наружный диаметр и .

4.3 Пример выполнения расчетно-графической работы № 2.2: Внутренние усилия и перемещения при кручении

Дано: сплошной вал с (рис. 4.6)

Необходимо:

Источник

Статическое растяжение

Машина для испытаний на растяжение с электромеханическим приводом

Статическое растяжение — одно из наиболее распространённых видов испытаний для определения механических свойств материалов.

Основные характеристики, определяемые при испытании[править | править код]

При статическом растяжении, как правило, определяются следующие характеристики материала.

• Характеристики прочности:
  • предел пропорциональности,
  • предел текучести,
  • предел прочности (временное сопротивление разрушению),
  • истинное сопротивление разрыву.
• Характеристики пластичности:
  • относительное остаточное удлинение,
  • относительное остаточное сужение.
• Характеристики упругости:
  • модуль упругости (модуль Юнга).
• Прочие характеристики:
  • коэффициент механической анизотропии
  • коэффициент (модуль) упрочнения

Основные типы материалов[править | править код]

Принято разделять пластичные и хрупкие материалы. Основное отличие состоит в том, что первые деформируются в процессе испытаний с образованием пластических деформаций, а вторые практически без них вплоть до своего разрушения. За критерий для условной классификации материалов можно принять относительное остаточное удлинение δ = (lк − l0)/l0, где l0 и lк — начальная и конечная длина рабочей части образца), обычно вычисляемое в процентах. В соответствии с величиной остаточного удлинения материалы можно разделить на:

• пластичные (δ ≥ 10 %);
• малопластичные (5 % < δ < 10 %);
• хрупкие (δ ≤ 5 %).

Существующие материалы могут быть изотропными или анизотропными. В последнем случае из-за различия характеристик в различных направлениях необходимо произвести не одно, а несколько испытаний.

Образцы для испытаний на статическое растяжение[править | править код]

Цилиндрический пятикратный образец

Цилиндрический пятикратный образец после разрушения

Для испытаний на статическое растяжение используют образцы как с круглым, так и с прямоугольным сечением. Предъявляются повышенные требования к изготовлению образцов, как с точки зрения геометрии, так и с точки зрения обработки резанием. Требуется высокая однородность диаметра образца по его длине, соосность и высокое качество поверхности (малая шероховатость, отсутствие царапин и надрезов). При изготовлении образцов следует избегать перегрева материала и изменений его микроструктуры.

Образцы круглого сечения, как правило, имеют рабочую длину, равную четырём или пяти диаметрам — т. н. короткие образцы или десяти диаметрам — т. н. нормальные образцы. Перед началом испытания замеряется диаметр образца (обычно 6, 10 или 20 мм) для вычисления напряжения σ и для расчёта относительного остаточного сужения после разрушения образца. В случае использования экстензометра, длина рабочей части образца не замеряется, а деформация ε и относительное удлинение при разрушении регистрируются автоматически с помощью компьютера или измеряются по диаграмме σ — ε. При отсутствии экстензометра (не рекомендуется стандартом), отмечается рабочая длина образца, деформация ε рассчитывается по перемещениям конца образца (захвата), а относительное удлинение при разрушении рассчитывается путём замера разрушенного образца.

Диаграмма растяжения пластичного материала[править | править код]

Рис. 1. Типичная диаграмма σ — ε для малоуглеродистой стали

1. Предел прочности (временное сопротивление разрушению)

2. Предел текучести (верхний)

3. Точка разрушения

4. Область деформационного упрочнения

5. Образование шейки на образце

Рис. 2. Типичная диаграмма σ — ε для алюминиевых сплавов

1. Предел прочности (временное сопротивление разрушению)

2. Условный предел текучести (σ0.2)

3. Предел пропорциональности

4. Точка разрушения

5. Деформация при условном пределе текучести (обычно, 0,2 %)

Микроструктура доэвтектоидной стали (0,7 % углерода)

Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl. Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A0, где A0 — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l0 ). Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.

Начальный участок является линейным (т. н. участок упругой деформации). На нём действует закон Гука:

Затем начинается область пластической деформации. Эта деформация остаётся и после снятия приложенной нагрузки. Переход в пластическую область обнаруживается не только по проявлению остаточных деформаций, но и по уменьшению наклона кривой с увеличением степени деформации. Данный участок диаграммы обычно называют площадкой (зоной) общей текучести, так как пластические деформации образуются по всей рабочей длине образца. С целью изучения и точного анализа диаграммы деформации, современные испытательные машины оснащены компьютеризированной записью результатов.

По наклону начального участка диаграммы рассчитывается модуль Юнга. Для малоуглеродистой стали наблюдается т. н. «зуб текучести» и затем площадка предела текучести. Явление «зуба» текучести связано с дислокационным механизмом деформации. На начальном участке плотность дислокаций является недостаточной для обеспечения более высокой степени деформации. После достижения точки верхнего предела текучести начинается интенсивное образование новых дислокаций, что приводит к падению напряжения. Дальнейшая деформация при пределе текучести происходит без роста напряжения . Зависимость предела текучести, от размера зерна, d, выражена соотношением Холла-Петча:

После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации. В этой области до достижения максимальной нагрузки (напряжения (σВ) макродеформация остаётся равномерной по длине испытуемого образца. После достижения точки предела прочности начинает образовываться т. н. «шейка» — область сосредоточенной деформации. Расположение «шейки» зависит от однородности геометрических размеров образца и качества его поверхности. Как правило, «шейка» и, в конечном счёте, место разрушения расположено в наиболее слабом сечении. Кроме того, важное значение имеет одноосность напряжённого состояния (отсутствие перекосов образца в испытательной машине). Для пластичных материалов при испытании на статическое растяжение одноосное напряжённое состояние сохраняется лишь до образования т. н. «шейки» (до достижения максимальной нагрузки и начала сосредоточенной деформации).

Вид диаграммы деформации, приведённый на рис. 1 является типичным для О.Ц.К. материалов с низкой исходной плотностью дислокаций.

Для многих материалов, например, с Г. Ц. К. кристаллической решёткой, а также для материалов с высокой исходной плотностью дефектов, диаграмма имеет вид, показанный на рис. 2. Основное отличие — отсутствие явно выраженного предела текучести. В качестве предела текучести выбирается значение напряжения при остаточной деформации 0,2 % (σ0.2).

После достижения максимума нагрузки происходит падение нагрузки (и, соответственно, напряжения σ) за счёт локального уменьшения площади поперечного сечения образца. Соответствующий (последний) участок диаграммы называют зоной местной текучести, так как пластические деформации продолжают интенсивно развиваться только в области шейки.

Иногда используется диаграмма истинных напряжений, S — e (истинное напряжение S = P/A, где A — текущая площадь поперечного сечения образца; истинная деформация e = ln(l+Δl/l), где l — текущая длина образца). В этом случае, после достижения максимальной нагрузки не происходит падения напряжения, истинное напряжение растёт за счёт локального уменьшения сечения в «шейке» образца. Поэтому различие между диаграммами истинных и условных напряжений наблюдается только после предела прочности — до точки 1 они практически совпадают друг с другом.

Образцы из пластичного материала разрушаются по поперечному сечению с уменьшением диаметра в месте разрыва из-за образования «шейки».

Диаграмма растяжения хрупкого материала[править | править код]

Диаграмма растяжения и диаграмма условных напряжений хрупких материалов по виду напоминает диаграмму, показанную на рис. 2 за тем исключением, что не наблюдается снижения нагрузки (напряжения) вплоть до точки разрушения. Кроме того, данные материалы не получают таких больших удлинений как пластичные и по времени разрушаются гораздо быстрее. На диаграмме хрупких материалов уже на первом участке имеется ощутимое отклонение от прямолинейной зависимости между нагрузкой и удлинением (напряжением и деформацией), так что о соблюдении закона Гука можно говорить достаточно условно. Так как пластических деформаций хрупкий материал не получает, то в ходе испытания не определяют предела текучести. Не имеет особенного смысла также рассчитывать и относительное сужение образца, так как шейка не образуется и диаметр после разрыва практически не отличается от исходного.

Влияние скорости деформации и температуры на прочностные характеристики[править | править код]

Стандарты на проведение испытаний на статическое растяжение, как правило, ограничивают скорость деформации или скорость приложения нагрузки. Так, стандарт ASTM E-8 ограничивает скорость деформации величиной 0,03 — 0,07 мм/мин. Такое ограничение вызвано искажением результатов за счёт повышения прочности металлов с ростом скорости деформации (при постоянной температуре). При скоростях деформации до 1 сек скорость деформации практически не влияет на прочностные характеристики (в частности, на предел текучести) (источник???).

В общем виде можно выразить формулу влияния скорости деформации на предел текучести в виде:

где — скорость деформации; — астотный фактор, — активационный объём; — напряжение течения; — экстраполяция напряжения течения на нулевую скорость деформации.

Эта же зависимость даёт и зависимость напряжения течения от температуры. В области низких температур и при отсутствии фазовых превращений прочность кристаллических материалов повышается. Вклад в повышение прочности даёт и переход от термически активируемого процесса деформации за счёт движения дислокаций к механизму деформации путём двойникования.

Стандарты на проведение испытаний[править | править код]

• ГОСТ 6996-66
• ГОСТ 1497-84 Металлы. Методы испытаний на растяжение
• ГОСТ 11262-80 (СТ СЭВ 1199-78) Пластмассы. Метод испытания на растяжение
• ASTM E-8 и ASTM E-8M

Литература[править | править код]

• Я. Б. Фридман. Механические свойства металлов. 3-е изд. В 2-х ч. М.: Машиностроение, 1974
• М. Л. Бернштейн, В.А Займовский. Механические свойства металлов. 2-е изд. М.: Металлургия, 1979.
• А. Н. Васютин, А. С. Ключ. Влияние температуры и скорости деформации на сопротивление деформированию малоуглеродистых и низколегированных сталей. Заводская лаборатория, 1985, № 4.

См. также[править | править код]

• Растяжение-сжатие

Источник