Формула растяжения пружины 7 класс
Содержание статьи
Сила упругости
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Источник
Сила упругости. Закон Гука. 7-й класс
Цель урока: выяснить природу силы упругости, сформулировать закон Гука.
Задачи:
- обучающие: сформировать знанияо деформации, силе упругости; вывести закон Гука; сформировать способности применять закон Гука при решении задач.
- развивающие: продолжить формирование у учащихся представлений о разнообразии сил в природе, развивать умение наблюдать и объяснять физические явления; проводить эксперимент, делать выводы;
- воспитательные: продолжить формирование навыков коллективной и самостоятельной работы, развивать чувства товарищеской взаимопомощи, ответственности за проделанную работу.
Оборудование: компьютер, экран, мультимедиапроектор, Презентация, 4 штатива с муфтами и лапками, набор грузов по 1Н, 2 разные пружины, 2 разные резинки, прибор для демонстрации видов деформации, резиновые и пластилиновые игрушки, губка, эспандер, гибкие металлические или пластмассовые линейки, 12 полосок бумаги шириной 6-7 см, карточки с заданиями.
Предварительная подготовка: разделить учащихся на 4 группы.
Ход урока
I. Актуализация знаний.
Слайд 2
- Какая сила действует на все тела, находящиеся на Земле?
- Какая сила действует на снег, лежащий на крыше дома; на человека, лежащего в гамаке; на груз, висящий на тросе?
- Что изменяется у тела, на которое действует сила?
- Почему снег, человек, груз не падают? (на них действует сила, которая не дает упасть)
Учитель: Мы должны выяснить, что это за сила, из-за чего возникает, к какой точке приложена, куда она направлена, от чего зависит, чему равен ее модуль.
II. Изучение нового материала:
Учитель: У вас на столе лежат различные резиновые и пластилиновые предметы. Что произойдет с ними, если вы их сожмете, растяните, надавите на них? Что у них изменилось?
А если прекратить воздействовать на резиновые и пластилиновые предметы, что произошло?
Слайды3-4
Показ видов деформаций на приборе для демонстрации видов деформации.
Задание группам:
Положите металлическую или пластмассовую линейку на опоры, поставьте на нее груз.
Подвесьте грузик к пружине, резинке.
Учитель: Что пронаблюдали?
Почему прогнулась (деформировалась) линейка, если положить на нее груз?
А почему через некоторое время прогибание останавливается?
Что произойдет, если снять груз?
Почему?
Почему растянулись пружина или резинка, если подвесить груз?
Почему через некоторое время растяжение останавливается?
Что произойдет, если снять груз?
Почему?
К чему приложена возникающая сила?
Куда она направлена?
Слайд 5
Выясним, в чем же причина возникновения силы упругости:
- Как называются частицы, из которых состоят вещества?
- Какие взаимодействия существуют между молекулами?
- На каком расстоянии действует сила притяжения?
- На каком расстоянии действует сила отталкивания?
Причиной возникновения сил упругости является взаимодействие молекул тела. На малых расстояниях молекулы отталкиваются, а на больших – притягиваются. В недеформированном теле молекулы находятся как раз на таком расстоянии, при котором силы притяжения, либо силы отталкивания уравновешиваются. Когда мы растягиваем или сжимаем тело, расстояния между молекулами изменяются, поэтому начинают преобладать либо силы притяжения, либо силы отталкивания. В результате и возникает сила упругости, которая всегда направлена так, чтобы уменьшить величину деформации тела.
Слайд 6
Сила упругости – это электромагнитная сила, возникающая при деформации тела и направленная в сторону, противоположную направлению смещения частиц тела при деформации. Приложена к деформируемому телу.
Слайд 7. Начертить в тетради:
Учитель: Если тело лежит на опоре, то сила упругости обозначается N – сила реакции опоры.
Выясним, от чего зависит сила упругости (на столах у групп учащихся стоят штативы с подвешенными пружинами, резинками, грузы).
Задание группам:
- Измерить длину нерастянутой пружины (резинки) l0.
- Подвесить к пружине (резинке) один груз, отметить силу 1 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Подвесить к пружине (резинке) второй груз, отметить силу 2 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Подвесить к пружине (резинке) третий груз, отметить силу 3 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Постройте график зависимости силы упругости от удлинения и сделайте вывод.
Вывод: чем больше сила, тем больше удлиняется пружина.
Слайды 8-10
Учитель: Какая зависимость между силой упругости и удлинением?
Для упругих или пластических деформаций выполняется данная зависимость?
Учитель: В 1660 году английский ученый Роберт Гук, когда ему было 25 лет, установил закон зависимости силы упругости от упругих деформаций, названный впоследствии его именем.
Но опубликовал он этот закон спустя 16 лет, проделав ряд экспериментов подтвердивших данный закон.
Сила упругости, возникающая при упругой деформации тела, прямо пропорциональна величине деформации) Δl и направлена в сторону противоположную перемещению частиц тела при деформации.
Fупр = k ∙ Δl
В законе Гука Δl – удлинение [м], k – коэффициент жесткости [H/м]
Учитель: всем видам деформации подвержено и человеческое тело, и при этом также возникает сила упругости.
Слайд 11 Физкультминутка:
Встали, потянулись (деформация растяжения/сжатия)
Наклоны вправо, влево, вперед, назад (деформация изгиба)
Повороты головы, кистей рук, плеч, туловища (деформация кручения)
Учитель: У каждого тела своя жесткость. От чего зависит коэффициент жесткости?
Задание группам:
- Укоротите пружину (или резинку), подвесьте грузик. Сильно растянулась пружина (резинка)? Что больше растянулось?
- Как увеличить прочность (жесткость) листочка бумаги? (на столах у групп учащихся листочки бумаги)
Учащиеся пробуют изменить форму. - Сделайте вывод.
Вывод: жесткость деформируемого тела зависит от материала, размеров и формы.
Учитель: Как же учитывают жесткость материала при строительстве? Слайды 12-17
Учитель: Людям каких профессий кроме строителей нужно учитывать силу упругости? Где применяются знания об этой силе? Слайды 18-27
Также и в природе учитывается существование деформаций и силы упругости. Кажется небольшой лес, а на самом деле …
Учитель: Как вы определяете, жесткий хлеб или мягкий?
Почему говорят стул жесткий? Кресло мягкое?
А где в животном мире используется сила упругости (домашнее задание)
III. Рефлексия.
Учитель: подведем итоги:
- Какие виды деформаций мы изучили?
- Перечислить особенности действия силы упругости:
- когда возникает? (возникает при упругих деформациях)
- куда направлена? (направлена противоположно направлению смещения)
- к чему приложена? (к деформируемому телу)
- при каких деформациях выполняется закон Гука? (при упругих деформациях).
Слайд 28 Задачи по группам:
1. Под действием какой силы пружина, имеющая коэффициент жесткости 1 кН/м, сжалась на 4 см?
2. Определите удлинение пружины, если на нее действует сила 10 Н, а коэффициент жесткости пружины 500 Н/м.
3. Чему равен коэффициент жесткости стержня, если под действием груза 1000 Н он удлинился на 1 мм?
4. По своим графикам определить коэффициент жесткости пружины (или резинки).
Слайд 29
IV. Д.з.
§25, задания 25.1 — 25.6 рабочей тетради; если не успели в классе, то дорешать задачи.
V. Выставление оценок.
Литература, интернет-ресурсы:
- С.Е. Полянский Поурочные разработки по физике 7 класс. – Москва «Вако», 2003.
- Учебно-методический комплекс А.В. Перышкина.
- ЦОР iles.school-collection.edu.ru/dlrstore/669b2b61-e921-11dc-95ff-0800200c9a66/3_13.swf
Источник
Задачи на тему «Сила упругости. Закон Гука» с решениями
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
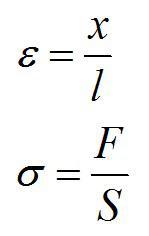
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
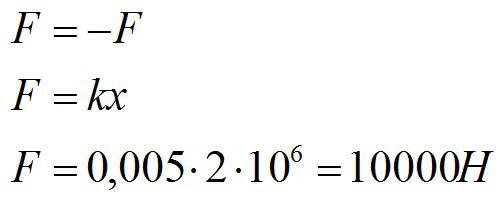
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
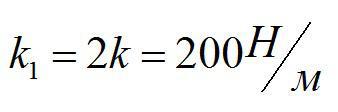
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
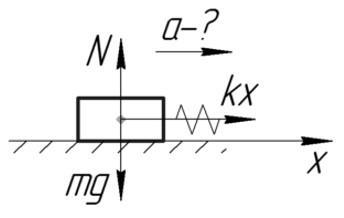
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
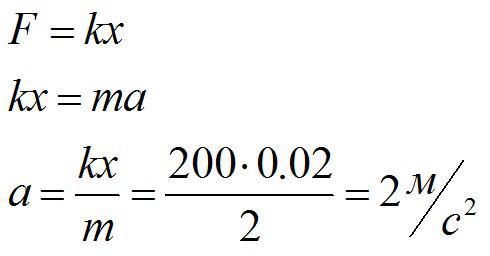
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
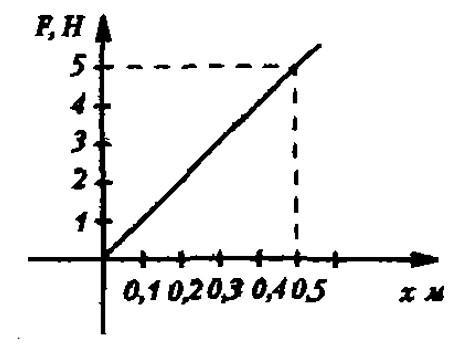
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
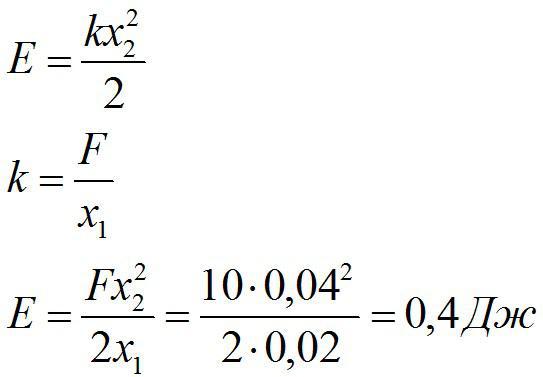
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Источник
