Как найти растяжение динамометра
Содержание статьи
Сила упругости
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Источник
Сила упругости
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
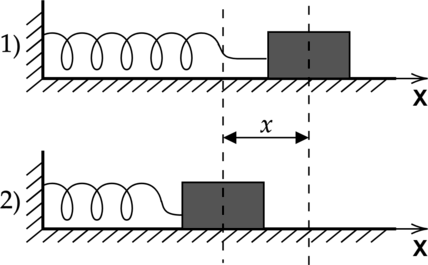
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
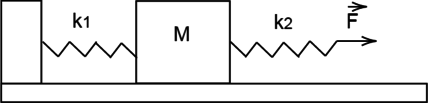
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
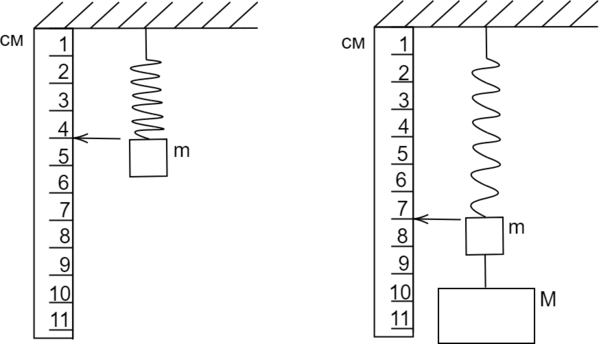
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
Сила упругости. Вес тела – FIZI4KA

1. Твёрдые тела под действием силы способны изменять свои форму и (или) объём. Взяв за концы металлическую линейку, можно её согнуть. Если перестать прикладывать силу, то линейка восстановит свою форму. Если сжать пружину (рис. 35), то она сократится, т.е. деформируется. При прекращении действия силы пружина вернётся в первоначальное
состояние.
Изменение формы или объёма тела при действии на него силы называется деформацией.
Если длина пружины в недеформированном состоянии ( l_0 ), а после растяжения ( l ), то изменение её длины ( l=l-l_0=x ), где ( l ) или ( x ) – удлинение или деформация.
2. При деформации в теле возникает сила упругости, которая стремится вернуть его в первоначальное состояние. Сила упругости ( (vec{F}_{упр}) ) — сила, возникающая в теле в результате деформации, стремящаяся вернуть тело в первоначальное состояние и направленная в сторону, противоположную деформации (удлинению).
Так, при растяжении пружины эта сила направлена влево к положению равновесия, при
сжатии пружины сила упругости направлена вправо (рис. 36).
Если тело после прекращения действия силы принимает первоначальную форму, то деформация является упругой. Если тело после прекращения действия силы не принимает первоначальную форму, то деформация является неупругой или пластической.
3. При малых деформациях сила упругости прямо пропорциональна удлинению. Поскольку сила упругости и деформация направлены в противоположные стороны, то: ( F_{упр}=-kDelta l ), где ( k ) — коэффициент пропорциональности, называемый жёсткостью тела. Жёсткость зависит от размеров тела, его формы, материала, из которого сделано тело.
Единица жесткости ( [,k,]=frac{[,F,]}{[,Delta l,]} ); ( [,k,]=frac{1,Н}{1,м}=1frac{Н}{м} ).
Формула ( F_{упр}=-kDelta l ) выражает закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации.
Важно понимать, что закон Гука справедлив при малых деформациях.
На рисунке 37 приведён график зависимости модуля силы упругости от деформации. Поскольку эта зависимость линейная, то графиком зависимости является прямая, проходящая через начало координат и составляющая угол ( alpha ) с осью абсцисс. По графику можно определить жёсткость тела. Например, значению деформации 2 см соответствует сила упругости 4 Н. Разделив 4 Н на 0,02 м, получим ( k ) = 200 Н/м. В треугольнике АОВ жёсткость ( k ) равна тангенсу угла ( alpha ): ( k=mathrm{tg}alpha ).
4. Существуют разные виды деформации: растяжения, сжатия, сдвига, изгиба и кручения. В рассмотренных примерах линейка подвергалась деформации изгиба, пружина — деформации растяжения и сжатия, винты, гайки, болты при закручивании испытывают деформацию кручения, тяжёлые предметы при перемещении по полу — деформацию сдвига.
5. Предположим, что на полу стоит ящик (рис. 38). На него действует сила тяжести ( vec{F}_т ), направленная вертикально вниз. Ящик, взаимодействуя с полом, деформирует его и деформируется сам. И на ящик, и на пол действует сила упругости, характеризующая их взаимодействие. Сила упругости ( vec{N} ), действующая на ящик со стороны пола, приложена к ящику и направлена вертикально вверх; сила упругости ( vec{P} ), действующая со стороны ящика на пол, приложена к полу и направлена вертикально вниз. Эта сила называется весом тела.
Весом тела называют силу, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес. В отличие от силы тяжести, вес тела приложен не к телу, а к опоре или к подвесу. Вес — это сила упругости.
6. Если тело покоится или движется равномерно и прямолинейно, вес тела численно равен силе тяжести, действующей на него: ( vec{P}=mvec{g} ).
На тело, движущееся вместе с платформой или подвесом вертикально вниз с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_{т} ) и сила упругости ( N ) со стороны опоры или подвеса (рис. 39, 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=ma ) или ( N=mg-ma ). Поскольку ( N=P ), ( P = m(g — a) ).
Если тело движется вниз вместе с опорой или подвесом с ускорением, направленным так же, как и ускорение свободного падения, то его вес меньше силы тяжести, т.е. меньше веса покоящегося тела. Если ускорение тела равно ускорению свободного падения ( vec{a}=vec{g} ), то тело находится в состоянии невесомости.
В таком состоянии находится космонавт в космическом корабле, прыгун с трамплина во время полёта вниз.
7. На тело, движущееся вместе с платформой или подвесом вертикально вверх с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_т ) и сила упругости ( vec{N} ) со стороны опоры или подвеса (рис. 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=-ma ) или ( N=mg+ma ). Поскольку ( N=P ), ( P=m(g+a) ).
Таким образом, если тело движется вверх вместе с опорой или подвесом с ускорением, направленным противоположно ускорению свободного падения, то его вес больше силы тяжести, т.е. больше веса покоящегося тела. Увеличение веса тела при движении с ускорением называют перегрузкой. Перегрузки испытывают космонавт в космическом корабле, пилот реактивного самолёта при взлёте и посадке.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость ( k_2 ) второй пружины с жёсткостью ( k_1 ) первой пружины.
1) ( k_1=k_2 )
2) ( 4k_1=k_2 )
3) ( 2k_1=k_2 )
4) ( k_1=2k_2 )
2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости ( F_2 ), возникающую во второй пружине, с силой упругости ( F_1 ), возникающей в первой пружине, при одинаковом их удлинении.
1) ( F_2=F_1 )
2) ( F_2=4F_1 )
3) ( 2F_2=F_1 )
4) ( 0.5F_2=F_1 )
3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.
1) 0,02 Н/м
2) 0,5 Н/м
3) 2 Н/м
4) 50 Н/м
4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.
1) ( k_2=k_1 )
2) ( k_2>k_1 )
3) ( k_2<k_1 )
4) ( k_2geq k_1 )
5. Учащийся выполнял эксперимент по измерению удлинения ( x ) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин ( k_1 ) и ( k_2 ) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?
1) ( k_2=4k_1 )
2) ( k_1=2k_2 )
3) ( k_2=2k_1 )
4) ( k_1=k_2 )
6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?
1) 3,5 Н
2) 4 Н
3) 4,5 Н
4) 5 Н
7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины ( k_1 ) в 2 раза больше жесткости второй пружины ( k_2 ). Удлинение первой пружины ( Delta l_1 ), удлинение второй пружины ( Delta l_2 ) равно
1) ( 0.5Delta l_1 )
2) ( 0.67Delta l_1 )
3) ( 1.5Delta l_1 )
4) ( 2.5Delta l_1 )
8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика
1) равен модулю силы тяжести
2) больше модуля силы тяжести
3) меньше модуля силы тяжести
4) увеличивается с увеличением скорости лифта
9. Человек испытывает перегрузки при
1) равномерном движении вниз
2) равномерном движении вверх
3) равноускоренном движении вверх из состояния покоя
4) равноускоренном движении вниз с ускорением свободного падения
10. Различие веса тела на экваторе и на полюсе можно обнаружить
А. Взвешивая тело на рычажных весах
Б. Взвешивая тело на пружинных весах
Правильный ответ
1)только А
2)только Б
3) и А, и Б
4) ни А, ни Б
11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Модуль силы упругости пружины
Б. Жёсткость пружины
B. Модуль удлинения пружины
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется
12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.
1) Закон Гука справедлив при любых деформациях.
2) Сила упругости направлена в сторону, противоположную деформации.
3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести.
5) Вес приложен к опоре или к подвесу.
Часть 2
13. Груз массой 5 кг начинают поднимать вертикально вверх с ускорением 2 м/с2. Чему равен вес груза?
Ответы
Сила упругости. Вес тела
3 (60%) 6 votes
Источник
