Как рассчитать силу растяжения пружины
Содержание статьи
Расчет пружин сжатия и растяжения
ФОРМУЛЫ И СПОСОБЫ РАСЧЕТА ПРУЖИН
ИЗ СТАЛИ КРУГЛОГО СЕЧЕНИЯ
(по ГОСТ 13765-86)

МЕТОДИКА ОПРЕДЕЛЕНИЯ РАЗМЕРОВ ПРУЖИН ПО ГОСТ 13765-86
1. Исходными величинами для определения размеров пружин являются силы F1 и F2 , рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении
или при разгрузке vmax, выносливость Np и наружный диаметр пружины D1 (предварительный).Если задана только одна F2 сила то вместо рабочего хода h для подсчета берут величину рабочей деформации S 2, соответствующую заданной силе.
2. По величине заданной выносливости Np предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с учето значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной — из ГОСТ 1071-81.
7. По полученным значениям F3и τ3, a также по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vk и
отношение vmax / vk, подтверждающее или отрицающее принадлежность пружины к предварительно установленному классу. При несоблюдении условий vmax / vk < 1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия.
Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1 и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)-(25).
КЛАССЫ И РАЗРЯДЫ ПРУЖИН
Ниже рассматриваются винтовые цилиндрические пружины сжатия и растяжения из стали круглого сечения с индексами i = d/D от 4 до 12.
Приводимые данные распространяются на пружины для работы при температурах от -60 до +120°С в неагрессивных средах. Пружины разделяют на классы, виды и разряды (см. ниже).
Класс пружин характеризует режим нагружения и выносливости, а также определяет основные требования к материалам и технологии изготовления.
Разряды пружин отражают сведения о диапазонах сил, марках применяемых пружинных сталей, а также нормативах по допускаемым напряжениям.
Отсутствие соударения витков у пружин сжатия определяется условием vmax / vk < 1,
где,
vmax — наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке, м/с;
vk — критическая скорость пружин сжатия, м/с (соответствует возникновению соударения витков пружины от сил инерции).
ВЫНОСЛИВОСТЬ И СТОЙКОСТЬ ПРУЖИН
При определении размеров пружин необходимо учитывать, что при vmax> vk, помимо касательных напряжений кручения, возникают контактные напряжения от соударения витков, движущихся по инерции после замедления и остановок сопрягаемых с пружинами деталей. Если соударение витков отсутствует, то лучшую выносливость имеют пружины с низкими напряжениями τ3, т.е. пружины класса I по табл. 1, промежуточную — циклические пружины класса II и худшую — пружины класса III.
При наличии интенсивного соударения витков выносливость располагается в обратном порядке, т.е. повышается не с понижением, а с ростом τ3. В таком же порядке располагается и стойкость, т.е. уменьшение остаточных деформаций или осадок пружин в процессе работы.
1. КЛАССЫ ПРУЖИН по ГОСТ 13765-86
| Класс пружин | Вид пружин | Нагружение | Выносливость NF (установленная безотказная наработка), циклы, не менее | Инерционное соударение витков |
| I | Сжатия и растяжения | Циклическое | 1×107 | Отсутствует |
| II | Циклическое и статическое | 1×105 | ||
| III | Сжатия | Циклическое | 2×103 | Допускается |
Примечание. Указанная выносливость не распространяется на зацепы пружин растяжения.
2. РАЗРЯДЫ ПРУЖИН по ГОСТ 13765-86
| Сила пружины при максим. деформации F3, H | Диаметр проволоки (прутка) d, мм | Материал | Твердость после термообработки HRC | Максимальное касательное напряжение при кручении τ3, МПа | ||||||
| Марка стали | Стандарт на заготовку | |||||||||
| I | 1 | 1 — 850 | 0,2 — 5,0 | по ГОСТ 1050 и ГОСТ 1435 | Проволока класса I по ГОСТ 9389 | — | 0,3Rm | ГОСТ 13766 | ||
| 2 | 1 — 800 | Проволока классов II и IIА по ГОСТ 9389 | ГОСТ 13767 | |||||||
| 22,4 — 800 | 1,2 — 5,0 | 51ХФА-Ш по ГОСТ 14959 | Проволока по ГОСТ 1071 | 0,32Rm | ||||||
| 3 | 140 — 60000 | 3,0 — 12,0 | 60С2А, 65С2ВА, 70СА3 по ГОСТ 14959 | Проволока по ГОСТ 14963 | 47,5…53,5 | 560 | ГОСТ 13768 | |||
| 51ХФА по ГОСТ 14959 | Проволока по ГОСТ 14963 | 45,5…51,5 | ||||||||
| 4 | 2800 — 180000 | 14 — 70 | 60С2А, 65С2ВА, 70С3А, 60С2, 60С2ХА, 60С2ХФА, 51ХФА по ГОСТ 14959 | Сталь горячекат. круглая по ГОСТ 2590 | 44,0…51,5 | 480 | ГОСТ 13769 | |||
| II | 1 | 1,5 — 1400 | 0,2 — 5,0 | по ГОСТ 1050 и ГОСТ 1435 | Проволока класса I по ГОСТ 9389 | — | 0,5Rm | ГОСТ 13770 | ||
| 2 | 1,25 — 1250 | Проволока класса II и IIA по ГОСТ 9389 | ГОСТ 13771 | |||||||
| 37,5 — 1250 | 1,2 — 5,0 | 51ХФА-Ш по ГОСТ 14959 | Проволока по ГОСТ 1071 | 0,52Rm | ||||||
| 3 | 236 — 10000 | 3,0 — 12,0 | 60С2А, 65С2ВА по ГОСТ 14959 | Проволока по ГОСТ 14963 | 47,5…53,5 | 960 | ГОСТ 13772 | |||
| 65Г по ГОСТ 14959 | Проволока по ГОСТ 2771 | |||||||||
| 51ХФА по ГОСТ 14959 | Проволока по ГОСТ 14963 | 45,5…51,5 | ||||||||
| 4 | 4500 — 280000 | 14 — 70 | 60С2А, 60С2, 65С2ВА, 70С3А, 51ХФА, 65Г, 60С2ХФА, 60С2ХА по ГСТ 14959 | Сталь горячекат. круглая по ГОСТ 2590 | 44,0…51,5 | 800 | ГОСТ 13773 | |||
| III | 1 | 12,5 — 1000 | 0,3 — 2,8 | по ГОСТ 1050 и ГОСТ 1435 | Проволока класса I по ГОСТ 9389 | — | 0,6Rm | — | ГОСТ 13774 | |
| 2 | 315 — 14000 | 3,0 — 12,0 | 60С2А, 65С2ВА, 70С3А по ГОСТ 14959 | Проволока по ГОСТ 14963 | 54,5…58,0 | 13509 | ГОСТ 13775 | |||
| 3 | 6000 — 20000 | 14 — 25 | 60С2А, 65С2ВА, 70С3А по ГОСТ 14959 | Сталь горячекат. круглая по ГОСТ 2590 | 51,5…56,0 | 1050 | ГОСТ 13776 | |||
Примечания:
1. Максимальное касательное напряжение при кручении приведено с учетом кривизны витков.
2. Rm — предел прочности пружинных материалов
Средствами регулирования выносливости и стойкости циклических пружин в рамках каждого класса при неизменных заданных значениях рабочего хода служат изменения разности между максимальным касательным напряжением при кручении τ3 и касательным напряжением при рабочей деформации τ2.
Возрастания разности τ3 — τ2 обусловливают увеличение выносливости и стойкости
циклических пружин всех классов при одновременном возрастании размеров узлов.
Уменьшение разностей τ3 — τ2 сопровождается обратными изменениями служебных качеств и размеров пространств в механизмах для размещения пружин.
Для пружин I класса расчетные напряжения и свойства металла регламентированы так, что при
νmax/ νk ≤ 1 обусловленная выносливость пружин при действии силы F1 (сила пружины при предварительной деформации) не менее 0,2F3 (сила пружины при максимальной деформации) обеспечивается при всех осуществимых расположениях и величинах рабочих участков на силовых диаграммах разности напряжений τ3 — τ2, и τ2 — τ1, (касательное напряжение при предварительной деформации).
Циклические пружины II класса при νЕЙ ПРУЖИН СЖАТИЯ И РАСТЯЖЕНИЯ
1. Пружина сжатия из проволоки круглого сечения с неподжатыми и нешлифованными крайними витками.
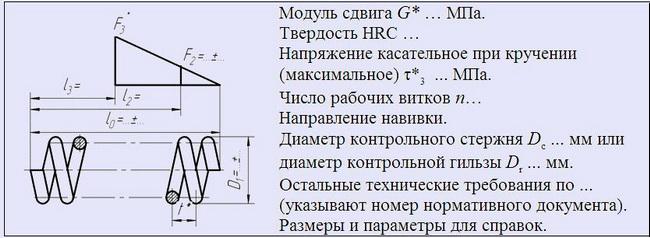
2. Пружина сжатия с поджатыми по 3/4 витка с каждого конца и шлифованными на 3/4 окружности опорными поверхностями.

3. Пружины растяжения из проволоки круглого сечения с зацепами, открытыми с одной стороны и расположенными в одной плоскости.
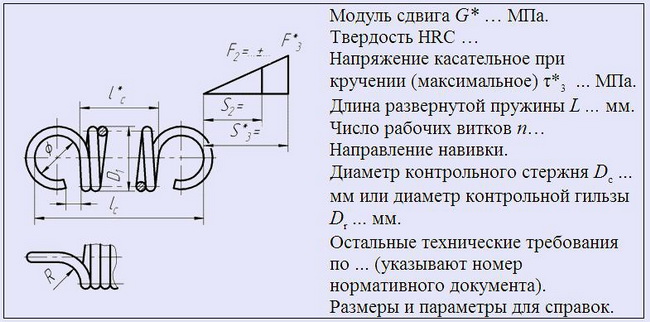
ОПОРНЫЕ ВИТКИ ПРУЖИН СЖАТИЯ
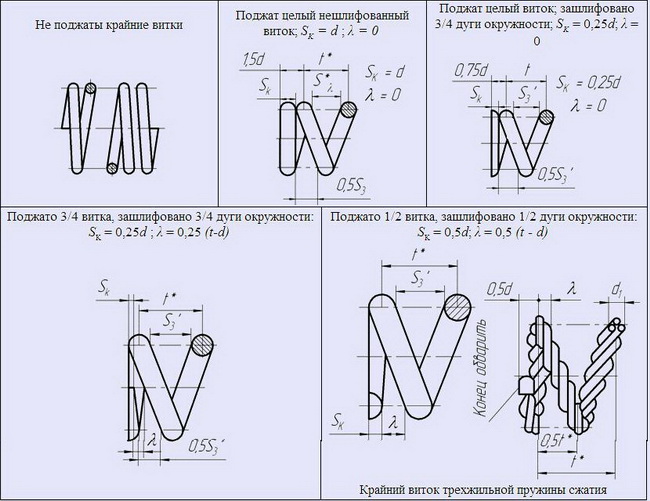
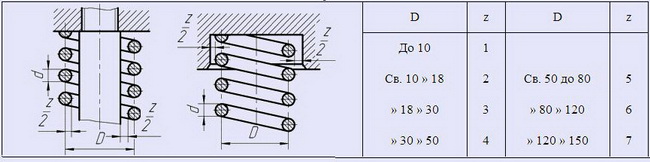
ДЛИНА ПРУЖИН СЖАТИЯ
Длину пружин сжатия рекомендуется принимать Lo <= (D1 — d).
Можно брать Lo до 5 х (D — d), но тогда пружины должны работать на направляющем стержне или в направляющей гильзе. При этом между пружиной и сопрягаемой деталью выдерживают зазор z в зависимости от величины среднего диаметра D пружины.
Значение зазора z, мм
Похожие документы:
чертеж пружины сжатия;
чертеж пружины параболоидной;
расчет пластинчатой пружины изгиба;
расчет пружин кручения из круглой проволоки;
ГОСТ 13764-86 » Пружины винтовые цилиндрические сжатия и растяжения из стали круглого сечения. Классификация»;
ГОСТ 13766-86 «Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 1 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13767-86 «Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 2 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13768-86 «Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 3 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13769-86 «Пружины винтовые цилиндрические сжатия 1 класса, разряда 4 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13770-86 «Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 1 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13771-86 «Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 2 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13772-86 «Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 3 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13773-86 «Пружины винтовые цилиндрические сжатия II класса, разряда 4 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13774-86 «Пружины винтовые цилиндрические сжатия III класса, разряда 1 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13775-86 «Пружины винтовые цилиндрические сжатия III класса, разряда 2 из стали круглого сечения. Основные параметры витков»;
ГОСТ 13776-86 «Пружины винтовые цилиндрические сжатия III класса, разряда 3 из стали круглого сечения. Основные параметры витков».
Источник
Калькулятор расчета пружин сжатия онлайн, изготовление по ГОСТ
Тип пружины
Материал
Вариант формирования зацепов
Диаметр проволоки (d) *
мм
Диаметр наружный (D нар.) *
мм
Длина пружины по зацепам (LO) *
мм
Длина пружины по телу (LO`) *
мм
Предварительное растяжение (L1)
мм
Рабочее растяжение (L2)
мм
Рабочее растяжение (L3)
мм
Количество пружин *
шт
Значения отмеченные * обязательны для заполнения.
Все расчетные данные несут информационно-ознакомительный характер.
Мой вес: 0.39875 кг.
Материал: 60С2А 51ХФА
Вариант зацепа: Удлинённый зацеп
D(вн)=
48.00
L0=64
L0*=38
D(нар)=64
d=8
F1=1830.90
F2=6713.31
F3=0.00
L1=94
L2=110
L3=0
| Диаметр средний (Dср.) | 56.00 мм |
| Диаметр внутренний (D вн.) | 48.00 мм |
| Внутренняя длина зацепа | 48.00 мм |
| Количество рабочих витков (n) | 3.75 шт |
| Количество витков полное (n1) | 5.75 шт |
| Предварительная нагрузка (F1) | 1830.90 H |
| Рабочая нагрузка (F2) | 6713.31 H |
| Рабочая нагрузка (F3) | 0.00 H |
| Жёсткость пружины (с) | 61.03 H/мм |
| Шаг (t) | 8 мм |
| Развертка пружины | 1011.08 мм |
| Масса пружины (m1) | 0.39875 кг |
| Вес партии (m2) | 717.76 кг |
https://metizdetal.beget.tech/
Источник
Расчет пружин | Справочник для конструкторов, инженеров, технологов
Для пружин сжатия классов I и II
δ = 0,05 — 0,25
для пружин растяжения
δ = 0,05 — 0,10
для одножильных пружин класса III
δ = 0,10 — 0,40
для трехжильных класса III
δ = 0,15 — 0,40
Уточняется по таблицам ГОСТ 13766 ÷ ГОСТ 13776
s» (при F0 > 0)
Для трехжильных пружин
Для трехжильных пружин
G = 7,85 х 104
где g — ускорение свободного падения, м/с2
γ — удельный вес, Н/м3
Для пружинной стали ρ = 8•103
Для пружин с предварительным напряжением
Для трехжильных пружин
где n2 — число опорных витков
Для трехжильных пружин
Для трехжильных пружин
Рекомендуется назначать от 4 до 12
| i | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 7,0 и более |
| Δ | 1,029 | 1,021 | 1,015 | 1,010 | 1,005 | 1,000 |
где n3 — число обработанных витков
Для трехжильных пружин
Для пружин растяжения с зацепами
Для пружин растяжения
Для пружин растяжения
Для трехжильных пружин
Для пружин растяжения
Для трехжильных пружин
Для пружин растяжения с предварительным напряжением
Источник
Сила упругости
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Источник
