Какая из формул выражает закон гука при растяжении

Сопротивление материалов

Деформации при растяжении и сжатии



Продольные деформации при растяжении и сжатии

Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:

ε = Δl / l

Относительное удлинение – величина безразмерная, иногда его выражают в процентах.

Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.

***

Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически эта зависимость записывается так:

σ = E ε.

Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).

Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.

Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:

Δl = Nl / (EА).

Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.

Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.

Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:

Δl = Σ (Δli)

***



Поперечные деформации при растяжении и сжатии

Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.

Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:

|ε1| = ν |ε|,

где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.

Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.

***

Потенциальная энергия деформации при растяжении

При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.

Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:

U = W = F Δl / 2 = N2 l / (2E А)

Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.

При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.

Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).

***

Материалы раздела «Растяжение и сжатие»:

• Основные понятия о деформации растяжения и сжатия.
• Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.

Смятие



Правильные ответы на вопросы Теста № 5

Определение и формула закона Гука

Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации.

Математическая запись закона выглядит так:

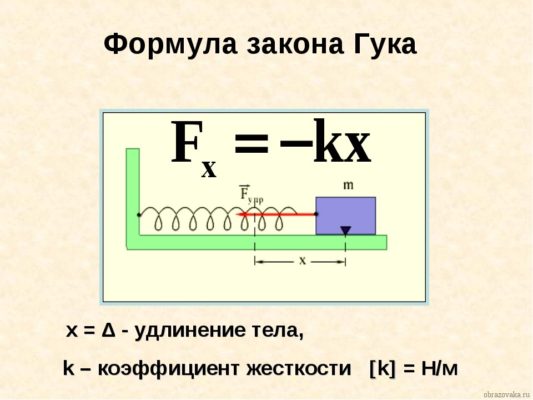
Рис. 1. Формула закона Гука

где Fупр – соответственно сила упругости, x – удлинение тела (расстояние, на которое изменяется исходная длина тела), а k – коэффициент пропорциональности, называемый жесткостью тела. Сила измеряется в Ньютонах, а удлинение тела – в метрах.

Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее получив выражение для k.

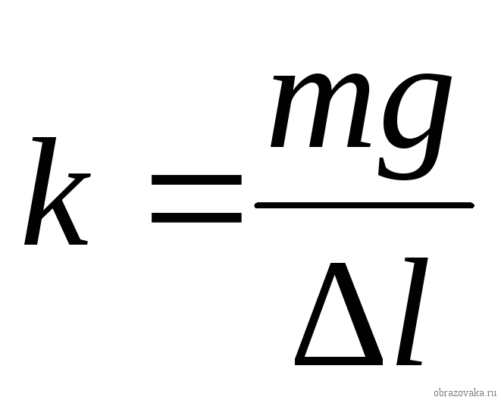
Рис. 2. Формула жесткости тела

Эта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле (пружине), когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.

Сила упругости

Теперь, когда известно, какая формула выражает закон Гука, необходимо разобраться в его основной величине. Основной величиной является сила упругости. Она появляется в определенный момент, когда тело начинает деформироваться, например, когда пружина сжимается или растягивается. Она направлена в обратную сторону от силы тяжести. Когда сила упругости и сила тяжести, действующие на тело, становятся равными, опора и тело останавливаются.

Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.

Особенности сил упругости

Как мы уже выяснили, сила упругости возникает при деформации, и направлена она на восстановление первоначальных форм и размеров строго перпендикулярно к деформируемой поверхности. У сил упругости также есть ряд особенностей.

• они возникают во время деформации;
• они появляются у двух деформируемых тел одновременно;
• они находятся перпендикулярно поверхности, по отношению к которой тело деформируется.
• они противоположны по направлению смещению частиц тела.

Применение закона на практике

Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.

Рис. 3. Динамометр

Тест по теме