Логические связки дизъюнкция отрицание импликация эквиваленция
Содержание статьи
Основы логики. Логические операции и таблицы истинности — Сайт-портфолио Уварова А.А.
Основы логики. Логические операции и таблицы истинности
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | ||
| 1 | ||
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 1 | |
| 1 | 1 | |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬A.
Таблица истинности для инверсии
| A | ¬А |
| 1 | |
| 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | ||
| 1 | 1 | |
| 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
«A ↔ B» истинно тогда и только тогда, когда А и B равны.
Обозначение: F = A ↔ B.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | ||
| 1 | ||
| 1 |
6) Операция XOR (исключающие или)
«A ⊕ B» истинно тогда, когда истинно А или B, но не оба одновременно.
Эту операцию также называют «сложение по модулю два».
Обозначение: F = A ⊕ B.
A B F 1 1 1 1 1 1 0
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…).
В общем случае таблицы истинности имеют размер
2N строк комбинаций для N независимых логических переменных.
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
| № | Для ИЛИ, / | Для И, & | Примечание |
| 1 | A / 0 = A | A & 1 = A | Ничего не меняется при действии, константы удаляются |
| 2 | A / 1 = 1 | A & 0 = 0 | Удаляются переменные, так как их оценивание не имеет смысла |
| 3 | A / B = B / A | AB = BA | Переместительный (коммутативности) |
| 4 | A / ¬A = 1 | Один из операторов всегда 1 (закон исключения третьего) | |
| 5 | A & ¬A = 0 | Один из операторов всегда 0 (закон непротиворечия) | |
| 6 | A / A = A | A & A = A | Идемпотентности (NB! Вместо A можно подставить составное выражение!) |
| 7 | ¬¬А = A | Двойное отрицание | |
| 8 | (A / B) / C = A / (B / C) | (A / B) / C = A / (B / C) | Ассоциативный |
| 9 | (A / B)&C=(A&C)/(B&C) | (A&B) / C = (A / C)&(B / C) | Дистрибутивный |
| 10 | (A / B)&(¬A / B) = B | (A&B) / (¬A&B) = B | Склеивания |
| 11 | ¬(A / B) = ¬A &¬B | ¬(A&B) = ¬A / ¬B | Правило де Моргана |
| 12 | A / (A&C) = A | A&(A / C) = A | Поглощение |
| 13 | A→B = ¬A / B и A→B = ¬B→¬A | Снятие (замена) импликации | |
| 14 | 1) A↔B = (A&B) / (¬A&¬B) 2) A↔B = (A / ¬B)&(¬A / B) | Снятие (замена) эквивалентности | |
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
A
→ B = ¬A / B
Для замены операции эквивалентности существует два правила:
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Логические выражения и множества
На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула
( (x ∈ А) → (x ∈ P) ) / (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
- [0, 3]
- [3, 11]
- [11, 15]
- [15, 17]
Решим уравнение: ( (x ∈ А) → (x ∈ P) ) / (x ∈ Q)=1 методом подстановки.
В уравнение вместо P, Q впишем сами отрезки: [2, 10] и [6, 14].
(x ∈ А)=1 для всех вариантов.
| Вариант ответа | Интервал A | Значения x для проверки (границы интервала) | ((x ∈ А) → (x ∈ [2, 10]) ) / (x ∈ [6, 14]) |
|---|---|---|---|
| 1 | [0, 3] | 0, 3 | (1→0)/0=0 (1→1)/0=1 |
| 2 | [3, 11] | 3, 11 | (1→1)/0=1 (1→0)/1=1 |
| 3 | [11, 15] | 11, 15 | (1→0)/1=1 (1→0)/0=0 |
| 4 | [15, 17] | 15, 17 | (1→0)/0=0 (1→0)/0=0 |
Ответ 2 вариант [3,11]
Источник
Логические операции и их свойства
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Обозначение: &, $wedge$, $cdot$.
Таблица истинности для конъюнкции
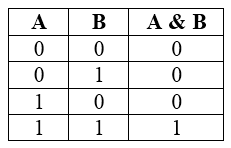
Рисунок 1.
Свойства конъюнкции:
- Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
- Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
- Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Обозначение: +, $vee$.
Таблица истинности для дизъюнкции
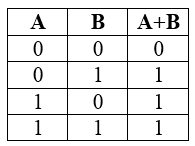
Рисунок 2.
Свойства дизъюнкции:
- Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
- Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
- Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Отрицание — означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.
Обозначения: не $A$, $bar{A}$, $¬A$.
Таблица истинности для инверсии
Рисунок 3.
Свойства отрицания:
«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.
Импликация или логическое следование
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).
Обозначения: $to$, $Rightarrow$.
Таблица истинности для импликации
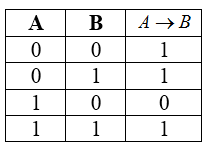
Рисунок 4.
Свойства импликации:
- $A to B = ¬A vee B$.
- Импликация $A to B$ ложна, если $A=1$ и $B=0$.
- Если $A=0$, то импликация $A to B$ истинна при любом значении $B$, (из лжи может следовать истинна).
Эквивалентность или логическая равнозначность
Эквивалентность — это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.
Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.
Таблица истинности для эквивалентности
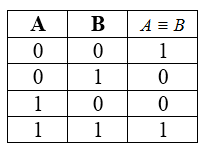
Рисунок 5.
Свойства эквивалентности:
- Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
- КНФ $A equiv B = (bar{A} vee B) cdot (A cdot bar{B})$
- ДНФ $A equiv B = bar{A} cdot bar{B} vee A cdot B$
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Обозначения: $A oplus B$ (в языках программирования), $A≠B$, $A wedge B$ (в языках программирования).
Таблица истинности для операции сложения по модулю два
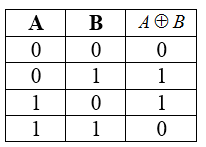
Рисунок 6.
Свойства строгой дизъюнкции:
- $a oplus 0 = a$(идемпотентность)
- $a oplus 1 = bar{a}$(отрицание)
- $a oplus a = 0$(получение 0)
- $a oplus b = b oplus a$(коммутативность)
- $(a oplus b) oplus c = a oplus (b oplus c)$(ассоциативность)
- $(a oplus b) oplus b = a$(поглощение)
- $bar{a} oplus b = a oplus bar{b} = (a equiv b)$(сравнения по модулю)
Стрелка Пирса
Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.
Обозначения: $downarrow$ , ИЛИ-НЕ
Таблица истинности для стрелки Пирса
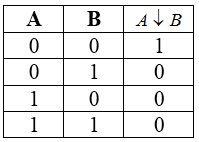
Рисунок 7.
Свойства:
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X downarrow X = ¬X$— отрицание
$(X downarrow Y) downarrow (X downarrow Y) equiv X vee Y$ — дизъюнкция
$(X downarrow X) downarrow (Y downarrow Y) equiv X wedge Y$ — конъюнкция
$((X downarrow X) downarrow Y) downarrow ((X downarrow X) downarrow Y) = X to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Обозначения: $|$, эквивалентно операции И-НЕ.
Таблицей истинности для функции штрих Шеффера
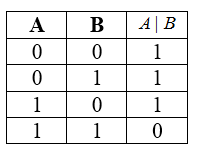
Рисунок 8.
Свойства:
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X mid X = ¬X$ — отрицание
$(X mid Y) mid (X mid Y) = (X wedge Y)$ — конъюнкция
$(X mid X) mid (Y mid Y) = X vee Y$ — дизъюнкция
$X mid ¬X$ — константа 1
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Для набора из $n$ логических переменных существует ровно $2^n$ различных значений. Таблица истинности для логического выражения от $n$ переменных содержит $n+1$ столбец и $2^n$ строк.
Источник
Основы формальной логики
Знакомы ли Вы с понятием «формальная логика»? Что такое конъюнкция и дизъюнкция? А импликация? В статье будут рассмотрены данные понятия. Надеюсь статья будет Вам полезна.
Формальная логика (математическая логика) является важнейшей основой функционирования современных компьютеров. Мы используем законы формальной логики, когда делаем запрос на поиск информации в Интернете или базе данных или когда анализируем правильность математического вывода. Многие элементы компьютеров проектируются и работают на основе законов формальной логики. Её общепризнанным создателем является английский математик Джордж Буль (1815 – 1864). До работ Буля логика всегда считалась одним из разделов философии. Основы логики, как науки о законах и формах мышления, были заложены ещё в работах Аристотеля в 384 г. до н.э. Аристотель ввёл понятие силлогизма, сделав важный шаг в разработке логической дедукции и формализации логических рассуждений. Когда мы говорим о формальной логике, то имеем в виду, что анализируется правильность формы высказываний и умозаключений, а не их конкретное содержание.
Достижения Аристотеля в области логики не претерпели существенных изменений вплоть до XVII века. Впервые идеи обоснования логики на основе вычислений, подобно тому как мы оперируем символами в алгебре, были высказаны ещё в XVII веке Готфридом Лейбницем. Идеи Лейбница реализовал в своих работах Дж. Буль. В 1847 г. он опубликовал работу «Математический анализ логики», в которой высказал идею, что логика более близка к математике, чем к философии. Эта работа была чрезвычайно высоко оценена английским математиком Августом Де Морганом, который преподавал математику для Ады Лавлейс. В 1854 году Буль опубликовал работу «Исследование законов мышления, базирующихся на математической логике и теории вероятностей». Эти исследования Буля заложили основы алгебры логики или булевой алгебры. Ученый первым показал, что существует аналогия между алгебраическими и логическими действиями. Буль придумал систему обозначений и правил, пользуясь которыми, можно было закодировать любые высказывания, а затем манипулировать ими как обычными алгебраическими выражениями. Именно поэтому логику Буля часто называют математической логикой или Булевой алгеброй.
Рассмотрим основные понятия логики: суждение, понятие, простые и сложные высказывания. С помощью понятий мы раскрываем значение естественных или искусственных знаков, указываем классы, к которым принадлежат или не принадлежат мыслимые нами вещи. Умственное развитие – это способность переосмысливать старые и конструировать новые понятия. Только понятия делают нашу речь осмысленной. Мы имеем понятие о некоторой вещи, если знаем и можем словесно выразить, какие условия необходимы и достаточны для её однозначного определения.
Условие, определяющие некоторый класс вещей, называется необходимым, если все вещи из этого класса и, возможно, некоторые вещи из его дополнения удовлетворяют этому условию. Условие, определяющее некоторый класс вещей, называется достаточным, если некоторые (может быть и все) вещи из этого класса удовлетворяют этому условию, но ни одна вещь из дополнения класса не удовлетворяет ему.
В терминах свойств можно определить необходимость некоторого условия следующим образом: если некоторая вещь не может существовать без данного свойства, то это свойство необходимо для её существования. Если же из существования некоторого свойства можно сделать вывод о существовании некоторой вещи, то это свойство достаточно для этой вещи.
Суждения позволяют нам выразить разнообразные отношения между мыслимыми вещами. Мы имеем суждение о некоторой вещи, если можем выразить словесно её отношение к другой вещи или к себе самой.
Основная языковая форма суждения – повествовательное предложение. Суждение может быть истинным, ложным или неопределённым. Суждение (высказывание) является простым, если ни одна его часть не может рассматриваться как суждение. Простые суждения принято обозначать буквами: А, B, C, D
Любое простое суждение состоит из 4-х функционально различимых частей:
1) субъекта суждения (S) – класс вещей, о котором нечто утверждается;
2) предиката суждения (P) – класс вещей, который утверждается относительно субъекта; предикат выражает то, что утверждается относительно S;
3) утвердительной или отрицательной связки «есть» или «не есть», которая ставится между S и P;
4) слов «все», «некоторые», «ни один», которые ставятся перед субъектом.
Если простое суждение имеет форму, отличную от (1), то его можно преобразовать к этой форме.
Все простые суждения классифицируются как утвердительные и отрицательные, которые, в свою очередь, делятся на общие и частные: « Все студенты ходят на лекции», «Некоторые преподаватели читают детективы», «Ни один человек не хочет быть несчастливым», «Некоторые фрукты не растут в России».
Суждение истинно, если в нём утверждается связь между объектом и признаком, имеющая место в действительности, или отрицается связь, не имеющая места в действительности. Суждение ложно, если в нём утверждается связь между объектом и признаком, не имеющая места в действительности, или отрицается связь, которая имеет место в действительности. Истину и ложь обозначают по–разному: 1 или 0, T или F (от английского True и False), И или Л. Мы будем пользоваться обозначением 1, если суждение истинно: A =1. Ложное суждение обозначим нулём: B =0.
Сложные суждения состоят из нескольких простых, соединённых различными логическими союзами: «неверно, что A», « B и C», «A или D», « если B, то C », «или А или В». Например, «сегодня тихо и пасмурно». Сложные суждения можно выразить через простые, но не наоборот.
Связка «не А» или «неверно, что A» называется отрицанием. Отрицание суждения А является истинным, если А ложно, и ложным, если А истинно. Обозначают отрицание суждения А как «не А» или A , или not(A). Правила вычисления логической операции «отрицание» можно задать с помощью таблицы:
Связка «и» называется конъюнкцией высказываний A и B и принимает значений истина, только когда оба высказывания истинны, в других случаях конъюнкция принимает значение ложь. Обозначают конъюнкцию суждений A и B как A&B, A and B (в программировании), A ⁄ B (в учебниках по логике). Правила вычисления конъюнкции зададим с помощью таблицы истинности:
Конъюнкцию иногда называют логическим умножением: результат в третьем столбце формально можно получить как произведение чисел из 1- ого и 2-ого столбцов.
Логически связка «или» называется дизъюнкцией. Дизъюнкция двух высказываний А и В принимает значение «истина», если хотя бы одно из высказываний истинно, и значение «ложь», если оба высказывания ложны. Для дизъюнкции используют обозначение A ¤ B, в программировании используют обозначение A or B. Таблица истинности для дизъюнкции имеет вид:
Дизъюнкцию иногда называют логическим сложением. Связка «или» в дизъюнкции не имеет исключающего характера. В логике используется так называемая сильная дизъюнкция (исключающее или), которая на русском языке выражается с помощью связки «или А, или В». Она носит исключающий характер, т.к. принимает значение истина, когда операнды имеют разное логическое значение. Обозначается в программировании как A xor B; таблица истинности имеет вид:
Очевидно, что конъюнкция, дизъюнкция и сильная дизъюнкция являются коммутативными операциями, т.е.
A⁄B = B⁄A; A¤B = B¤A; A xor B = B xor A.
Справедливость этих формул следует из таблиц истинности: при перестановке первых двух столбцов таблицы мы получим в третьем столбце значения, совпадающие со значениями третьего столбца исходной таблицы. Сложные суждения эквивалентны, если они принимают одинаковые логические значения при одинаковых значения простых высказываний, входящих в них.
Логическая связка «если…, то ….» называется импликацией. Импликация высказываний «если A, то В» принимает значение ложь только в одном случае, когда А истинно, а В ложно. Импликация обозначается как AØB. Суждение А называется посылкой, В следствием. Иногда употребляются термины антецедент для посылки А и консеквент – для заключения В. Таблица истинности для импликации имеет вид:
Импликация не обладает свойством коммутативности. Это следует из таблицы истинности: если переставить столбцы 1 и 2, то значения в третьем столбце изменятся. Многие теоремы в математике имеют форму импликации. При доказательстве теорем вида A ØB мы доказываем, что ситуация, в которой из верной посылки А можно вывести ложное заключение В, невозможна. Например, «Если числовой ряд сходится, то его n–ый член стремится к нулю». Если теорема A ØB имеет место, то говорят, что В является логическим следствием А.
Эквиваленция – это логическая связка, которая выражается словами «А тогда и только тогда, когда В », «для А необходимо и достаточно В». Эквиваленция обозначается как А¨В и выражается через импликацию и конъюнкцию:
А¨В = (АØВ) ⁄ (BØA)
Эквиваленция принимает значение истина в случае, когда оба высказывания имеют одинаковые значения. Таблица истинности для эквиваленции имеет вид:
Многие теоремы в математике имеют форму эквиваленции. Такие теоремы называются критериям. Например, «Скалярное произведение ненулевых векторов P и Q равно нулю тогда и только тогда, когда эти векторы перпендикулярны».
Из нескольких простых высказываний с помощью логических операций можно составить более сложные высказывания. Для указания порядка выполнения логических действий можно использовать круглые скобки. Для однозначного прочтения логических выражений принят следующий приоритет выполнения операций (перечислены в порядке убывания приоритета): отрицание, конъюнкция, дизъюнкция, сильная дизъюнкция, импликация, эквиваленция. Отрицание – самая «сильная» операция. Например,
А ⁄ В ¤ С = (А ⁄ В) ¤ С; A ¤ В Ø С = (( A ) ¤ В) Ø С;
С помощью знака = (равно) будем обозначать равносильные высказывания – высказывания, которые принимают одинаковые логические значения при одинаковых значения простых высказываний, входящих в них. Логическое значение сложного высказывания определяется логическими значениями входящих в него простых высказываний. Например, требуется вычислить логическое значение сложного высказывания «не (А ⁄ В) ¤ (не С)» в случае, если А = 1, В = 1, С=0. Подставим на место простых высказываний их значения. Тогда А ⁄ В = 1, не (А ⁄ В) = 0, (не С ) = 1, дизъюнкция 0 ¤ 1 = 1. Заданное высказывание истинно при заданных значениях А, В, С.
Для определения всех возможных значений сложного высказывания, в зависимости от всевозможных значений входящих в него элементарных высказываний, можно построить таблицу истинности. В этой таблице для каждого простого высказывания, входящего в заданное сложное высказывание, надо создать отдельный столбец. Затем нужно заполнить строки таблицы для простых высказываний всевозможными комбинациями их логических значений. Если число простых высказываний равно n, то таких комбинаций будет 2n . Затем надо представить сложное высказывание в виде комбинации более простых, но также сложных высказываний и завести для каждого из них свой столбец. Один столбец (обычно последний) заводим для заданного высказывания. Заполняем все строки полученной таблицы. Например, пусть задано высказывание (формула)
не А ¤ В Ø А ⁄ не В.
Требуется составить для данного высказывания таблицу истинности. Запишем данную формулу с применением скобок: ((не А) ¤ В) Ø (А ⁄ (не В)). В таблице будет четыре строки, т.к. простых высказываний два: А и В.
Отметим, что заданная формула эквивалентна формуле «не (А Ø В)» (см. таблицу истинности для импликации), так как принимает одинаковые с ней логические значения при одинаковых значениях простых суждений, входящих в эти формулы. Перечислим основные правила преобразования логических выражений. Эти правила используются для упрощения заданных формул с целью получения из них более простых и эквивалентных им выражений.
4) А¨В = (АØВ) ⁄ (BØA)
В логике доказывается теорема, в которой утверждается, что все логические операции можно выразить через отрицание, конъюнкцию и дизъюнкцию. Говорят, что эти операции образуют полную систему логических операций.
Для операций конъюнкции и дизъюнкции имеют место свойства коммутативности, ассоциативности и дистрибутивности:
Рассмотрим пример равносильных преобразований. Упростить формулу, используя перечисленные выше свойства и правила преобразования логических выражений:
В XX веке в математической логике произошли важные изменения: впервые со времен своего возникновения логика стала многозначной. В многозначной логике высказывания могут иметь более двух истинностных значений. В 1920 г. Ян Лукасевич разработал трёхзначную логику. В ней высказывания могут принимать три значения: «истина», «ложь» и «может быть» или «неопределено». В такой логике не действует закон исключенного третьего. В 1921 г. Э. Пост выдвинул идею многозначной логики. В k – значной логике высказывания могут принимать значения от 0 до к-1, где k=3,4, 5… и т.д.
Подписывайтесь на мой блог и следите за появлением новых статей.
Учёба может быть легкой — просто зайди на мой блог!
Источник
