Приведите примеры использования деформации растяжения и сжатия
Содержание статьи
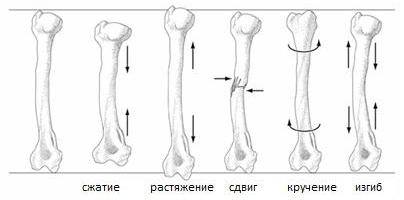
Деформация: сдвиг, растяжение, сжатие, кручение, изгиб. Примеры деформации
Деформация сдвига, кручения, изгиба – это изменение объема и формы тела при воздействии на него дополнительной нагрузки. При этом меняются расстояния между молекулами или атомами, приводящие к появлению сил упругости. Рассмотрим основные виды деформаций и их характеристики.

Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.
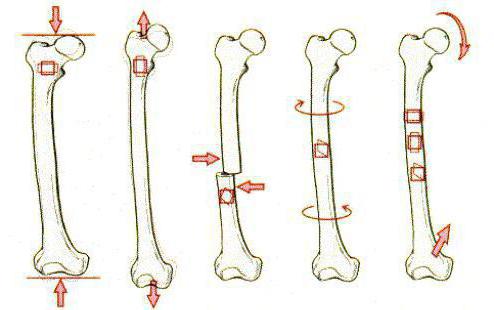
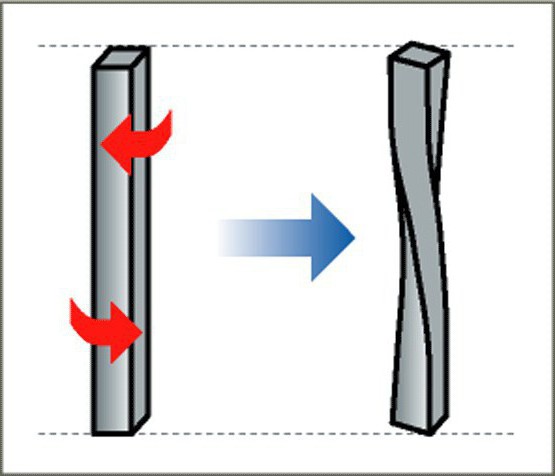
Деформация изгиба
Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.
В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.
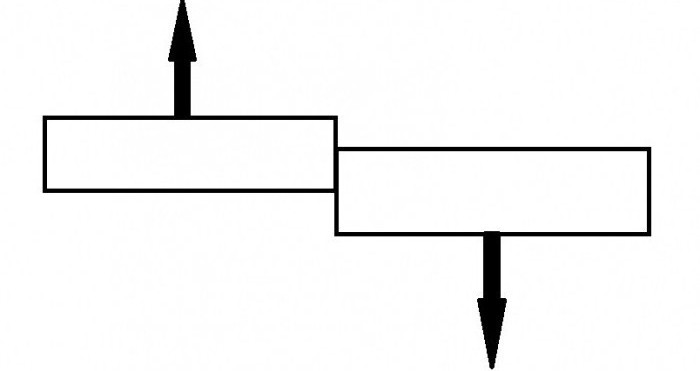
Деформация кручения
Эта продольная деформация является неоднородным сдвигом. Она возникает при действии сил, направленных параллельно либо противоположно на стержень, у которого закреплен один конец. Чаще всего сложным деформациям подвергаются различные детали и механизмы, применяемые в конструкциях и машинах. Но благодаря сочетанию нескольких вариантов деформаций, существенно облегчается вычисление их свойств.
Кстати, в процессе существенной эволюции кости птиц и животных приняли трубчатый вариант строения. Такое изменение способствовало максимальному упрочнению скелета при определенной массе тела.
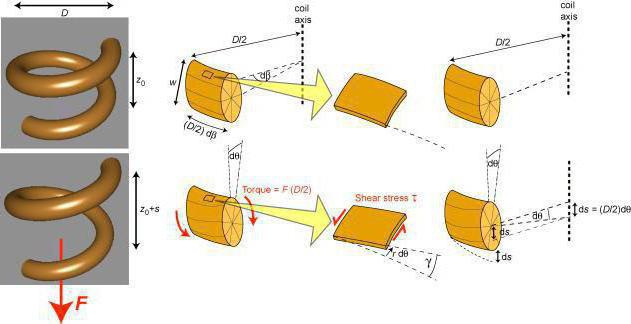
Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Закон Гука
Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.
По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.
Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.
Заключение
Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.
Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан. Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига. Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.
Источник
Деформация твёрдого тела: её виды, измерение
Деформация твёрдого тела: её виды, измерение
Подробности
Категория: Молекулярно-кинетическая теория
Опубликовано 17.11.2014 18:20
Просмотров: 12024
Под воздействием внешних сил твёрдые тела меняют свою форму и объем, т.е. деформируются.
В результате действия приложенных к телу сил частицы, из которых оно состоит, перемещаются. Изменяются расстояния между атомами, их взаимное расположение. Это явление называют деформацией.
Если после прекращения действия силы тело возвращает свою первоначальную форму и объём, то такая деформация называется упругой, или обратимой. В этом случае атомы снова занимают положение, в котором они находились до того, как на тело начала действовать сила.
Если мы сожмём резиновый мячик, он изменит форму. Но тут же восстановит её, как только мы его отпустим. Это пример упругой деформации.
Если же в результате действия силы атомы смещаются от положений равновесия на такие расстояния, что межатомные связи на них уже не действуют, они не могут вернуться в первоначальное состояние и занимают новые положения равновесия. В этом случае в физическом теле происходят необратимые изменения.
Сдавим кусочек пластилина. Свою первоначальную форму он не сможет вернуть, когда мы прекратим воздействовать на него. Он деформировался необратимо. Такую деформацию называют пластичной, или необратимой.
Необратимые деформации могут также происходить постепенно с течением времени, если на тело воздействует постоянная нагрузка, или под влиянием различных факторов в нём возникает механическое напряжение. Такие деформации называются деформациями ползучести.
Например, когда детали и узлы каких-то агрегатов во время работы испытывают серьёзные механические нагрузки, а также подвергаются значительному нагреву, в них со временем наблюдается деформация ползучести.
Под воздействием одной и той же силы тело может испытывать упругую деформацию, если сила приложена к нему на короткое время. Но если эта же сила будет воздействовать на это же тело длительно, то деформация может стать необратимой.
Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а само тело восстановит свою форму после снятия нагрузки, называется пределом упругости. При значениях выше этого предела тело начнёт разрушаться. Но разрушить твёрдое тело не так-то просто. Оно сопротивляется. И это его свойство называется прочностью.
Когда два автомобиля, соединённые буксировочным тросом, начинают движение, трос подвергается деформации. Он натягивается, а его длина увеличивается. А когда они останавливаются, натяжение ослабевает, и длина троса восстанавливается. Но если трос недостаточно прочный, он просто разорвётся.
Типы деформации
В зависимости от того, как приложена внешняя сила, различают деформации растяжения-сжатия, сдвига, изгиба, кручения.
Деформация растяжения-сжатия

Деформация растяжения-сжатия вызывается силами, которые приложены к концам бруса параллельно его продольной оси и направлены в разные стороны.
Под действием внешних сил частицы твёрдого вещества, колеблющиеся относительно своего положения равновесия, смещаются. Но этому процессу пытаются помешать внутренние силы взаимодействия между частицами, старающиеся удержать их в исходном положении на определённом расстоянии друг от друга. Силы, препятствующие деформации, называются силами упругости.
Деформацию растяжения испытывают натянутая тетива лука, буксировочный трос автомобиля при буксировке, сцепные устройства железнодорожных вагонов и др.
Когда мы поднимается по лестнице, ступеньки под действием нашей силы тяжести деформируются. Это деформация сжатия. Такую же деформацию испытывают фундаменты зданий, колонны, стены, шест, с которым прыгает спортсмен.
Деформация сдвига

Если приложить внешнюю силу по касательной к поверхности бруска, нижняя часть которого закреплена, то возникает деформация сдвига. В этом случае параллельные слои тела как бы сдвигаются относительно друг друга.
Представим себе расшатанный табурет, стоящий на полу. Приложим к нему силу по касательной к его поверхности, то есть, попросту потянем верхнюю часть табурета на себя. Все его плоскости, параллельные полу, сместятся друг относительно друга на одинаковый угол.
Такая же деформация происходит, когда лист бумаги разрезается ножницами, пилой с острыми зубьями распиливается деревянный брус и др. Деформации сдвига подвергаются все крепёжные детали, соединяющие поверхности, — винты, гайки и др.
Деформация изгиба

Такая деформация возникает, если концы бруса или стержня лежат на двух опорах. В этом случае на него действуют нагрузки, перпендикулярные его продольной оси.
Деформацию изгиба испытывают все горизонтальные поверхности, положенные на вертикальные опоры. Самый простой пример — линейка, лежащая на двух книгах одинаковой толщины. Когда мы поставим на неё сверху что-то тяжёлое, она прогнётся. Точно так же прогибается деревянный мостик, перекинутый через ручей, когда мы идём по нему.
Деформация кручения

Кручение возникает в теле, если приложить пару сил к его поперечному сечению. В этом случае поперечные сечения будут поворачиваться вокруг оси тела и относительно друг друга. Такую деформацию наблюдают у вращающихся валов машин. Если вручную отжимать (выкручивать) мокрое бельё, то оно также будет подвергаться деформации кручения.
Закон Гука

Наблюдения за различными видами деформации показали, что величина деформации тела зависит от механического напряжения, возникающего под действием приложенных к телу сил.
Эту зависимость описывает закон, открытый в 1660 г. английским учёным Робертом Гуком, которого называют одним из отцов экспериментальной физики.
Виды деформации удобно рассматривать на модели бруса. Это тело, один из трёх размеров которого (ширина, высота или длина), гораздо больше двух других. Иногда вместо термина «брус» употребляют термин «стержень». У стержня длина намного превышает его ширину и высоту.
Рассмотрим эту зависимость для деформации растяжения-сжатия.
Предположим, что стержень первоначально имеет длину L. Под действием внешних сил его длина изменится на величину ∆l. Она называется абсолютным удлинением (сжатием) стержня.
Для деформации растяжения-сжатия закон Гука имеет вид:
F — сила, сжимающая или растягивающая стержень; k — коэффициент упругости.
Сила упругости прямо пропорциональна удлинению тела до некого предельного значения.
Е — модуль упругости первого рода или модуль Юнга. Его величина зависит от свойств материала. Это теоретическая величина, введённая для характеристики упругих свойств тел.
S — площадь поперечного сечения стержня.
Отношение абсолютного удлинения к первоначальной длине стержня называют относительным удлинением или относительной деформацией.
При растяжении его величина имеет положительное значение, а при сжатии отрицательное.
Отношение модуля внешней силы к площади поперечного сечения стержня называется механическим напряжением.
Тогда закон Гука для относительных величин будет выглядеть так:
Напряжение σ прямо пропорционально относительной деформации ε.
Считается, что сила, стремящаяся удлинить стержень, является положительной (F ˃ 0), а сила, укорачивающая его, имеет отрицательное значение (F ˂ 0).
Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов.
Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.
Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.
В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.
В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.
Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.
Источник
Деформация растяжения-сжатия: характеристики, расчеты, параметры
В машиностроении, строительстве и архитектуре при расчетах прочности и жесткости материалов используется математический аппарат технической механики. Деформация растяжения – одно из ключевых понятий, характеризующее механические процессы, происходящие в материалах при приложении к ним внешних воздействий. Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.
Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:
Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).
Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.
При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.
Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
Напряжения при растяжении сжатии
Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:
Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.
Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:
Δl=Nl/EA
Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).
В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.
В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Расчеты на прочность и жесткость
Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.
Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.
Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.
Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.
С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.
С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.
При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.
Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.
Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.
Источник
