Прочность каменной кладки при растяжении срезе изгибе
Содержание статьи
ПРОЧНОСТЬ КЛАДКИ ПРИ РАСТЯЖЕНИИ, СРЕЗЕ И ИЗГИБЕ


Устал с поисками информации? Мы тебе поможем!
Материалы для каменной кладки
К искусственным каменным материалам относят кирпичи керамический и силикатный полнотелые и пустотелые, керамические и силикатные камни пустотелые и камни бетонные и гипсовые стеновые
Полнотелый керамический кирпич имеет размеры 250х120х65 мм и модульный (утолщенный) — 250х120х88 мм, масса кирпича 3,6…5 м. Плотность 1,6…1,8 т/м3, марки кирпича 75, 100, 150, 200, 250 и 300, водопоглощение до 8%. Кирпич изготовляют пластическим пpeccoванием с последующим обжигом. Основной недостаток — высокая теплопроводность.
Пустотелый, пористый и дырчатый кирпичи имеют при тех же размерах в плане высоту 65, 88, 103 и 138 мм (в 1,25, 1,5 и 2 раза большую высоту по сравнению с полнотелым кирпичом), меньшую плотность — 1,35…1,45 т/ м3. Марки кирпича — 75, 100 и 150. Применение этой разновидности кирпичей позволяет уменьшить массу стеновых изделий до 30%.
Силикатный кирпич применяют для стен с относительной влажностью не более 75%, марки кирпича — 75, 100 и 150. Кирпич изготовляют посредством прессования сырьевой смеси извести и кварцевого песка и последующей автоклавной обработки.
Керамические и силикатные пустотелые камни имеют размеры: (обычные — 250х120х 138 мм, укрупненные — 250х250х138 мм и модульные — 288х38х138 мм. Толщина камня соответствует двум кирпичам, уложенным на постель, с учетом толщины шва между ними. Поверхность камней бывает гладкой и рифленой.
Камни бетонные и гипсовые стеновые выпускают сплошными пустотелыми. Их изготовляют из тяжелых, облегченных и легких бетонов и гипсобетона с размерами 400х 200х200 мм, 400х200х90мм и массой до 35 кг.
2. На прочность кладки при сжатии влияют многие факторы, а именно:
а) прочность камня, б) размеры камня, в) правильность формы камня, г) наличие пустот в пустотелых камнях, д) прочность раствора, е) удобоукладываемость (подвижность) раствора при его применении, ж) упруго-пластические свойства (деформативность) затвердевшего раствора, з) качество кладки, и) перевязка кладки, к) сцепление раствора с камнем, л) степень заполнения вертикальных швов кладки.
Формула онищенко для определения прочности кладки при сжатии
ПРОЧНОСТЬ КЛАДКИ ПРИ РАСТЯЖЕНИИ, СРЕЗЕ И ИЗГИБЕ
Каменная кладка в зависимости от направления действующих усилий при работе на растяжение, изгиб и срез может разрушаться по неперевязанному или перевязанному сечению. Разрушение по неперевязанному сечению происходит по горизонтальному шву кладки ( 14.6,о), а по перевязанному сечению — либо по ступенчатому сечению ( 14.6,6, сечение 1—/), либо по плоскому сечению, пересекающему камни и вертикальные швы (
При изгибе кладка испытывает, с одной стороны, сжатие и, с другой, — растяжение. Здесь, так же как при осевом растяжении, возможна работа по неперевязанным ( 14.7,6) и перевязанным сечениям ( 14.7,а), Так как прочность кладки при сжатии значительно выше (в 10—20 раз), чем при растяжении, то временное сопротивление кладки при изгибе определяется ее работой в растянутой зоне. Возникающие здесь напряжения называют также главными растягивающими напряжениями Ягл при изгибе. Из опытов установлено, что временное сопротивление кладки растяжению при изгибе RpM по неперевязанному сечению в среднем в 1,5 раза больше сопротивления кладки осевому растяжению:
| 4. Расчет центрально сжатых элементов по несущей способности |
По несущей способности производят при равномерном распределении напряжений по сечению по следующей формуле:
(9)
где N – расчетная продольная сила;
mg – коэффициент, учитывающий снижение несущей способности вследствие ползучести кладки;
— коэффициент, учитывающий снижение несущей способности элемента за счет продольного изгиба, зависящего от гибкости элемента и упругой характеристики кладки ;
А – площадь поперечного сечения элемента
— отношение расчетной длины к радиусу инерции сечения
— для прямоугольного сечения (h – наименьший размер сечения)
Дата добавления: 2017-04-15; Мы поможем в написании ваших работ!; просмотров: 2294 | Нарушение авторских прав
| Изречения для студентов
Читайте также:
Поиск на сайте:
Рекомендуемый контект:

© 2015-2021 lektsii.org — Контакты — Последнее добавление
Источник
Прочность каменной кладки
● Прочность каменной кладки зависит от прочности и вида камня и раствора, возраста кладки, ее качества, обусловленного квалификацией каменщика, и других факторов. Опыты показывают, что даже при центральном сжатии камни и раствор в кладке находятся в условиях сложного напряженного состояния. Это объясняется тем, что поверхность кирпича или бетонного камня не является ровной, а раствор в швах имеет неодинаковую плотность и толщину (рис. 16.2). Работу камня можно представить как работу жесткого тела, покоящегося на многочисленных беспорядочно расположенных опорах. В таком теле возникают изгибающие моменты, поперечные силы, а также участки с местным смятием. Кроме того, поперечные деформации раствора, существенно (до 10 раз) превышающие деформации керамического кирпича, вызывают в нем растягивающие усилия, снижающие прочность кладки.
Различают прочность кладки при сжатии, растяжении, срезе, местном смятии. В расчет вводят сопротивление кладок различных видов на растворах разных марок, установленные в результате статистической обработки испытаний стандартных образцов. Характерные расчетные сопротивления приведены в табл. 16.1 и 16.2 [5].
Прочность кладки при сжатии R применяют при расчете стен, столбов, простенков. Установлено, что эта характеристика всегда меньше прочности камня, какой бы высокой прочности не использовался раствор. Например, расчетные сопротивления кладки сжатию кирпича М200 на растворе М100 составляют R=2,7 МПа, на растворе марки 10 — R = 1,6 МПа, а при нулевой прочности раствора — R = 1,0 МПа.
● Если кладка под нагрузкой испытывает осевое растяжение, то в зависимости от направления усилия может произойти разрушение по не-перевязанному сечению (рис. 16.3, а) либо по перевязанному сечению (рис. 16.3,6). Прочность по неперевязанному сечению ниже, чем по перевязанному. Прочность при осевом растяжении кладки Rt (табл. 16.2) используется, например, при расчете цилиндрических резервуаров.
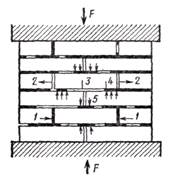
Рис. 16.2. Напряженное состояние камня в кладке:
1 — сжатие; 2 — растяжение; 3 — изгиб; 4 — срез; 5 — местное сжатие
Таблица 16.1.
Расчетные сопротивления сжатию кладки из
кирпича и керамических камней
| Марка кирпича иликамня | Расчетные сопротивления, МПа, сжатию кладки из кирпичаи керамических камней на тяжелых растворах | ||||||||
| при марке раствора | при прочностираствора | ||||||||
| 0,2 | нулевой | ||||||||
| 3,9 | 3,6 | 3,3 | 3,0 | 2,8 | 2,5 | 2,2 | 1.8 | 1,7 | 1,5 |
| 3,6 | 3,3 | 3,0 | 2,8 | 2,5 | 2,2 | 1,9 | 1,6 | 1,5 | 1,3 |
| 3,2 | 3,0 | 2,7 | 2,5 | 2,2 | 1,8 | 1,6 | 1,4 | 1,3 | 1.0 |
| 2,6 | 2,4 | 2,2 | 2,0 | 1,8 | 1,5 | 1,3 | 1,2 | 1,0 | 0,8 |
| — | 2,2 | 2,0 | 1,9 | 1,7 | 1,4 | 1,2 | 1,1 | 0,9 | 0,7 |
| — | 2,0 | 1,8 | 1.7 | 1,5 | 1,3 | 1,0 | 0,9 | 0,8 | 0,6 |
| — | — | 1,5 | 1,4 | 1,3 | 1,1 | 0,9 | 0,7 | 0,6 | 0,5 |
| — | — | — | 1,1 | 1,0 | 0,9 | 0,7 | 0,6 | 0,5 | 0,35 |
| — | — | — | 0,9 | 0,8 | 0,7 | 0,6 | 0,45 | 0,4 | 0,25 |
Таблица 16.2.
Расчетные сопротивления кладки из сплошных камней
| Вид напряженного состояния | Расчетные сопротивления, МПа,кладки из сплошных камней | ||||
| при марке раствора | при прочности раствора 0,2 | ||||
| 50 и выше | |||||
| Осевое растяжение Rt: | |||||
| по неперевязанному сечению (рис. 16.3, а) | 0,08 | 0,05 | 0,03 | 0,01 | 0,005 |
| по перевязанному сечению для кладки из камней правильной формы (рис. 16.3, б) | 0,16 | 0,11 | 0,05 | 0,02 | 0,01 |
| Растяжение при изгибе Rtb: | |||||
| по неперевязанному сечению | 0,12 | 0,08 | 0,04 | 0,02 | 0,01 |
| по перевязанному сечению (рис. 16.3, в) для кладки из камней правильной формы | 0,25 | 0,16 | 0,08 | 0,04 | 0,02 |
| Срез Rsq: | |||||
| по неперевязанному сечению | 0,16 | 0,11 | 0,05 | 0,02 | 0,01 |
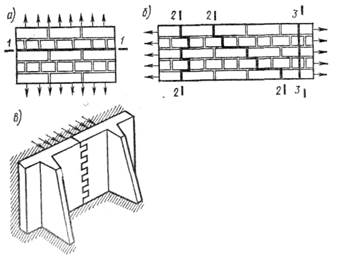
Рис. 16.3. Растяжение кладки:
а — по неперевязанному сечению; б — по перевязанному сечению; 1—1; 2—2 — проходящему по раствору; 3—3 — проходящему по кирпичу; в — растяжение кладки при изгибе
● В нормах приведены также расчетные сопротивления кладки на растяжение при изгибе Rtb и срезе Rsq (табл. 16.2), используемые, например, при расчете обсыпных подпорных стен с вертикальными контрфорсами (рис. 16.3, в).
Источник
Прочность каменных кладок при растяжении, изгибе, срезе. Модуль деформации кладки.
Прочность кладки при растяжении
Прочность каменных кладок при работе их на растяжение, срез и изгиб зависит, главным образом, от величины сцепления между раствором и камнем.
Различают два вида сцепления:
нормальное — S (рис. 6,а) и касательное — Т (рис. 6,б).
Эксперименты показали, что касательное сцепление в два раза больше нормального, то есть Т= 2 S
Рис.6. Виды сцепления: а – нормальное; б — касательное
Величина сцепления возрастает:
— с увеличением марки раствора;
— при более шероховатой поверхности камня;
-при более чистой поверхности камня;
— при увлажнении камня.
Сцепление нарастает во времени и достигает 100% через 28 суток.
В вертикальных швах кладки вследствие усадки раствора при твердении сцепление его с камнем значительно ослабляется или совсем нарушается с одной из прилегающих боковых поверхностей камня. Поэтому в расчетах сцепление в вертикальных швах не учитывается, а учитывается сцепление только в горизонтальных швах кладки.
В соответствии с касательным и нормальным сцеплением различают два вида растяжения кладки: растяжение по перевязанному и неперевязанному швам.
Растяжение кладки по неперевязанному шву (рис. 7, а) в чистом виде практически не встречается, а главным образом имеет место при работе кладки на внецентренное сжатие при больших эксцентриситетах, когда происходит растяжение кладки с одной стороны, как показано на рис. 7, б.
Рис.7. Растяжение кладки: а – по неперевязочному шву; б – с одной стороны
Растяжение кладки по перевязанному шву (рис. 8) встречается в конструкциях резервуаров. В этом случае разрыву сопротивляются только участки горизонтальных швов (вертикальные швы не учитываются), в которых действует касательное сцепление. Разрушение кладки может происходить по штрабе при слабых растворах и прочных камнях, либо по камням и частично по штрабе при прочных растворах и малой прочности камня.
Рис. 8. Растяжение кладки по перевязочному шву
Прочность кладки при срезе
Срез кладки так же, как и растяжение, может быть по перевязанному и неперевязанному швам.
При действии усилий вдоль горизонтальных швов (рис. 9, а)
Рис.9. Срез кладки по перевязанному и неперевязанному швам
Имеет место срез по неперевязанному шву, который встречается в подпорных стенах (рис. 9, б) или в пятовых сечениях арок (рис. 9, в). В этом случае сопротивление оказывает касательное сцепление раствора с камнем, а при сжимающих нормальных напряжениях в кладке сопротивление срезу увеличивается благодаря возникновению сопротивления от трения.
При действии усилий перпендикулярно горизонтальным швам (рис.10, а) имеет место срез по перевязанному шву, который встречается в консольных выступах (рис. 10, б). В этом случае учитывается сопротивление только камня срезу без учета вертикальных швов.
Рис.10. Действия усилий: а – перпендикулярно горизонтальным швам;
б – консольные выступы
Прочность кладки при изгибе
Изгиб в каменной кладке вызывает растяжение, которым и определяется прочность кладки по растянутой зоне. Однако если определить разрушающий момент как для упругого материала, приняв в растянутой зоне расчетное сопротивление (как для центрального растяжения), то разрушающий момент оказывается примерно в 1,5 раза меньше, чем при натурных испытаниях. Это объясняется тем, что момент внутренних усилий теоретически определялся, исходя из треугольной эпюры распределения нормальных напряжений, как для упругого тела (рис.11, а):
Рис.11. Эпюры распределения нормальных напряжений: а – для упругого тела; б – криволинейная
На самом же деле благодаря тому, что в кладке кроме упругих имеют место и пластические деформации, эпюра нормальных напряжений криволинейная (Рис. 11, б) и если ее принять прямоугольной (что очень близко к фактической эпюре), то получим:
то есть в 1,5 раза больше, чем при упругой работе. В практических расчетах пользуются формулами сопротивления материалов и момент сопротивления W определяют, как для упругого материала. Расчетное сопротивление кладки растяжению при изгибе по перевязанному сечению принимают примерно в 1,5 раза больше, чем расчетное сопротивление кладки при центральном растяжении .
На рис. 12 показана часть здания, левый угол которого получил осадку, что привело к образованию наклонных трещин в подоконных поясах.
Эти трещины являются следствием возникновения главных растягивающих напряжений при изгибе.
Рис.12. Образование трещин в стене при осадке здания
Деформативность кладки
В каменной кладке различают следующие деформации:
— объемные, возникающие во всех направлениях, вследствие усадки раствора и камня или от изменения температуры;
— силовые, развивающиеся, главным образом, вдоль направления действия силы.
Усадочные деформации кладки st зависят от материала кладки. Например, для кладки из обожженного глиняного кирпича усадку можно не учитывать ввиду ее малости, а для кладок из силикатного кирпича и бетонных камней st = 3•10-4.
Температурные деформации кладки также зависят от материала кладки и коэффициента линейного расширения кладки t. Например, для глиняного кирпича и керамических камней t = 0,5•10-5, а для силикатного кирпича и бетонных камней t = 1•10-5.
При действии нагрузки (силовые деформации) каменная кладка представляет собой упругопластический материал, и поэтому при действии нагрузки зависимость между напряжениями и деформациями не подчиняется закону Гука. Начиная с небольших напряжений в кладке, кроме упругих, развиваются и пластические деформации. Поэтому силовые деформации будут зависеть от характера приложения нагрузки и могут быть трех видов:
1) деформации при однократном нагружении кратковременной нагрузкой;
2) деформации при длительном действии нагрузки;
3) деформации при многократно повторных нагрузках.
Если каменную кладку нагружать очень быстро и довести до разрушения за несколько секунд, то в кладке возникнут только упругие деформации, и кладка будет работать как упругий материал, а зависимость между напряжениями и деформациями будет линейной.
Если каменную кладку в лабораторных условиях загружать в течение 1 часа постепенно до разрушения, то зависимость между напряжениями и деформациями получается нелинейной; для данного случая кривая зависимости показана на рис. 13.
Таким образом, полные деформации будут слагаться из упругих и неупругих. В этом случае модуль деформации кладки Е будет величиной переменной:
С возрастанием напряжения угол уменьшается последовательно, уменьшается и модуль деформаций.
Наибольшее значение модуль деформаций будет иметь при , то есть -это начальный или мгновенный модуль упругости, величина которого для данного вида кладки является постоянной.
Рис.13. Кривая зависимости
Экспериментально установлено, что начальный модуль деформации Е0 модуль упругости кладки пропорционален временному сопротивлению сжатия кладки – Ru:
; .
Здесь — упругая характеристика кладки, зависящая от вида кладки и прочности раствора; R — расчетное сопротивление сжатию кладки; — коэффициент, принимаемый равным 2, для кладки из кирпича, камней, блоков.
В практических расчетах модуль деформаций кладки принимается Е=0,5Е0 или Е = 0,6Е0 в зависимости от характера расчета.
При действии длительных нагрузок в кладке развиваются деформации ползучести, поэтому в практических расчетах модуль упругости Е0 уменьшается путем деления его на коэффициент ползучести, величина которого принимается от 1,8 до 4,0 в зависимости от вида кладки.
При многократно повторных нагрузках после некоторого числа циклов «нагрузка-разгрузка» пластические деформации выбираются, и материал начинает работать упруго с модулем упругости Е0, но только если напряжения не превосходят напряжений, при которых появляются трещины в кладке : .
Если же , то после некоторого количества циклов «нагрузка-разгрузка» деформации начинают неограниченно расти, и кладка разрушается.
Список литературы
1. СП 63.13330.2018 Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52-01-2003/Минстрой России. – М., 2013. – 147с.
2. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий курс: Учеб. для вузов. – 5-е изд., перераб. и доп. – М.: Стройиздат, 1991. – 767с.
3. Еременок П.Л., Еременок И.П. — Каменные и армокаменные конструкции. – Киев: Вища школа, 1981.
Читайте также:
Рекомендуемые страницы:

Вам нужно быстро и легко написать вашу работу? Тогда вам сюда…
©2015-2021 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2020-04-06 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
 Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ! Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ! Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ!
Источник
Основные факторы, влияющие на прочность кладки при сжатии. Прочность кирпичной кладки при растяжении, изгибе и срезе. Прочность кладки при местном сжатии.
Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
При центральном сжатии напряжения по сечению элемента распределяются равномерно. Разрушение таких элементов происходит в зависимости от их гибкости: коротких элементов — в результате исчерпания прочностных свойств кладки ( ), длинных элементов — в результате потери устойчивости при критических напряжениях ( ), меньших предела прочности кладки R .
Расчет прочности центрально-сжатых элементов каменных конструкций следует производить по формуле
, где N — расчетная продольная сила; m, — коэффициент, учитывающий влияние прогиба сжатых элементов на их несущую способность при длительной нагрузке; — коэффициент продольного изгиба; R — расчетное сопротивление кладки сжатию; А — площадь сечения элемента.
Коэффициент зависит от характеристики упругих свойств кладки а и гибкости элемента.
Коэфициент отражает влияние ползучести при длительном действии нагрузки:
Где — коэффициент, зависящий от гибкости элемента и принимается по таблице. — расчетная продольная сила от длительного действия нагрузки.
Подбор сечений центрально. сжатых неармированных элементов производят с помощью последовательных приближений. 3а даваясь маркой и видом камня и раствора по нормам, находят расчетные сопротивления камня сжатию. Приняв в первом приближении mg=1, =0,9, по формуле вычисляют размеры столба или стены. По найденным размерам определяют гибкость элемента, затем по табл. 11.4 и формуле уточняют значения т„и у и производят повторный расчет.
Внецентренное сжатие.
На внецентренное сжатие работают конструкции каменных зданий, в которых продольная сжимающая сила N приложена с эксцентриситетом. Опыты показывают, что характер напряженного состояния каменной кладки внецентренно сжатых элементов в основном зависит от эксцентриситета продольной силы e0. Пpи небольших эксцентриситетах все сечение сжато, эпюра напряжений имеет криволинейное очертание. По мере увеличения эксцентриситета сжимающие напряжения со стороны, удаленной от силы, уменьшаются, а затем меняют знак, т. е. на некоторой части сечения возникает растяжение. При достаточно больших эксцентриситетах даже при малых нагрузках напряжения в растянутой зоне элемента могут превысить предельное сопротивление кладки растяжению при изгибе и в растянутой зоне появятся горизонтальные трещины, распространяющиеся на некоторую глубину t (). После образования трещины продолжает работать под нагрузкой только часть сечения высотой h — t. Эксцентриситет приложения продольной силы N для этой части сечения оказывается уменьшенным на величину t/2, т. е. сечение работает в условиях, приближающихся к центральному сжатию. Поскольку сжимающие напряжения распределены по сечению неравномерно, временное сопротивление кладки сжатию достигается первоначально в краевых участках. Однако при этом несущая способность не исчерпывается, так как в наиболее нагруженных участках вследствие ползучести развиваются значительные деформации, и тогда включаются в работу менее загруженные участки сжатой зоны и тем самым повышают ее временное сопротивление по сравнению с временным сопротивлением при центральном сжатии. Это повышение учитывается при расчете коэффициентом , который для кирпичной кладки прямоугольного сечения находят из выражения ; при е=О (центральное сжатие) =1.
Вследствие сложности напряженного состояния внецентренно сжатых элементов при расчете их прочности исходят из эмпирических формул, основанных на следующих допущениях: растянутая зона, если она имеется, исключается из работы, напряжения в сжатой зоне считаются распределенными равномерно (рис. 12.3). С учетом гибкости, длительности действия нагрузки и эффекта обоймы расчетное условие имеет вид
, (12.3)
где N — расчетная продольная сила; R — расчетное сопротивление кладки сжатию; А, — площадь сжатой части сечения элемента при прямоугольной эпюре напряжений, определяемая из условия, что ее центр тяжести совпадает с точкой приложения продольной силы N.
Местное сжатие (смятие)
В случаях, когда опирание какой-либо конструкции происходит не по всему сечению каменной кладки стены, фундамента, а только по его части, имеет место местное сжатие кладки. Сопротивление каменной кладки местному сжатию больше чем осевому, т.к. прилегающие к нагруженному участку смежные незагруженные зоны препятствуют его деформации и тем самым увеличивают в той или иной его степени несущую способность. Расчетное сопротивление при смятие
где (12.6)
R — расчетное сопротивление кладки при осевом сжатии; A — площадь смятия (местного сжатия), на которую передается нагрузка (рис. 12.4); А — расчетная площадь сечения при местном сжатии; — коэффициент, учитывающий максимально допустимое увеличение — по отношению к R, зависящий от материала кладки и места приложения нагрузки, колеблется в пределах от 1 до 2. Несущую способность элемента при местном сжатии проверяют по формуле
где Nloc –продольная сжимающая сила от местной нагрузки, — коэффициент полноты эпюры давления от местной нагрузки: при равномерном распределении давления (передача нагрузки через распределительную плиту) =1, при треугольной эпюре (передача нагрузки через слой раствора) =0,5; d — коэффициент, учитывающий пластическую работу материала, для кирпичной и виброкирпичной кладки d= 1,5 — 0,5 .
Если под опорами огибаемых элементов не требуется установка распределительных плит, то допускается принимать без специального расчета =0,75 (для кладок из полнотелого кирпича, сплошных камней и крупных блоков из тяжелого бетона).
При совместном действии местной (опорные реакции балок, ферм и др.) и основной нагрузок (вес вышележащей кладки и нагрузка, передающаяся на эту «ладку) расчет на смятие производят раздельно: сначала только на местную нагрузку, потом — на сумму местной и основной нагрузок.
Изгиб
На изгиб работают наружные стены многоэтажных зданий при действии ветровой нагрузки, наружные плиты контрфорсных подпорных стен и другие элементы. расчет каменной кладки на изгиб производят, исходя из предположения ее упругой работы:
(12.8)
где М — расчетный изгибающий момент; R — расчетное сопротивление кладки растяжению при изгибе по перевязанному сечению (см. табл. 11.2); W — момент сопротивления сечения кладки при упругой ее работе. На действие поперечной силы изгибаемые элементы рассчитывают по формуле
где R — расчетное сопротивление кладки главным растягивающим напряжениям при изгибе; z — плечо внутренней пары сил, для прямоугольного сечения z=2/3h; Ь и h — размеры сечения. Проектирование элементов каменных конструкций, работающих на изгиб по неперевязанному сечению, не допускается.
Растяжение и срез
Каменные конструкции, работающие на осевое растяжение (например, стенки круглых резервуаров, силосов и других емкостей), рассчитывают на прочность по формуле
N<
где N — расчетная осевая сила при растяжении; — расчетное сопротивление кладки растяжению; А„— расчетная площадь сечения «нетто», т. е. за вычетом пустот в камнях.
Проектирование элементов каменных конструкций, работающих на осевое растяжение по неперевязанному шву, не допускается.
На срез по горизонтальному шву работают, например, элементы каменной кладки, воспринимающие распор от затяжки сводов. Сопротивление каменной кладки срезу по горизонтальным неперевязанным швам складывается из собственной несущей способности
19 Балочные сборные перекрытия. Компоновка конструктивной схемыперекрытия. Расчет и конструирование плит армированных сварными сетками, каркасами инапрягаемой арматурой.
В состав конструкции балочного панельного сборного перекрытия входят плиты и поддерживающие их балки, называемые ригелями, или главными балкам. Ригели опираются на колонны и стены; их направление может быть продольным (вдоль здания) или поперечным. Ригели вместе с колоннами образуют рамы.
В поперечном направлении перекрытие может иметь два-три пролета для гражданских зданий и пять-шесть пролетов для промышленных. Размеры пролета ригелей промышленных зданий определяются общей компоновкой конструктивной схемы перекрытия, нагрузкой от технологического оборудования.
Компоновка конструктивной схемы перекрытия заключается в выборе направления ригелей, установлении их шага, размеров пролета, типа и размеров плит перекрытий. При этом учитывают:
временную нагрузку, назначение здания, архитектурно-планировочное решение;
общую компоновку конструкции всего здания. В зданиях, где пространственная жесткость в поперечном направлении создается рамами с жесткими узлами, ригели располагают в поперечном направлении, а панели в продольном. В жилых и общественных зданиях ригели могут иметь продольное направление, а плиты — поперечное. В каждом случае выбирают соответствующую сетку колонн;
технико-экономические показатели конструкции перекрытия. Расход железобетона на перекрытие должен быть минимальным, а масса элементов и их габариты должны быть возможно более крупными и соответствующими грузоподъемности монтажных кранов и транспортных средств.
При проектировании разрабатывают несколько вариантов конструктивных схем перекрытия и на основании сравнения выбирают наиболее экономичную.
Общий расход бетона и стали на устройство железобетонного перекрытия складывается из соответствующего расхода этих материалов на плиты, ригели и колонны. Наибольший расход железобетона — около 65 % общего количества — приходится на плиты. Поэтому экономичное решение конструкции плит приобретает важнейшее значение.
Для предварительно напряженных плит применяют бетон класса B15, B25, для плит без предварительного напряжения — бетон класса B15, В20.
Расчет плит. Расчетный пролет плит Lо принимают равным расстоянию между осями ее опор (рис. 11.5); при опирании по верху ригелей Lо=L — Ь/2 (Ь — ширина ригеля); при опирании на полки ригелей Lo=L — а — Ь (а — размер полки). При опирании одним концом на ригель, другим на стенку расчетный пролет равен расстоянию от оси опоры на стене до оси опоры в ригеле.
Высота сечения плиты h должна быть подобрана так, чтобы наряду с условиями прочности были удовлетворены требования жесткости (предельных прогибов). При пролетах 5…7 м высота сечения плиты определяется главным образом требованиями жесткости.
Высоту сечения предварительно напряженных плит можно предварительно назначать равной: h=Lo/20— для ребристых, h=Lo/30 — для пустотных плит.
При расчете прочности по изгибающему моменту ширина ребра равна суммарной ширине всех ребер плиты; расчетную ширину сжатой полки принимают равной полной ширине панели. При малой толщине сжатой полки, когда ‘/h<0,1, ширина полки, вводимая в расчет, не должна превышать
где n — число ребер в поперечном сечении панели.
В ребристой панели ребрами вниз при толщине , но при наличии поперечных ребер, вводимую в расчет ширину полки принимают равной полной ширине панели.
Таким образом, расчет прочности плит сводится к расчету таврового сечения с полкой в сжатой зоне. В большинстве случаев нейтральная ось проходит в пределах толщины сжатой полки, поэтому, определив
, затем находят площадь растянутой арматуры
Расчетную ширину сечения плиты ребрами вверх принимают равной суммарной ширине ребер и расчет ведут как для прямоугольного сечения.
Поперечную арматуру плиты рассчитывают из условия прочности по наклонному сечению по расчетной ширине ребра b, равной суммарной ширине всех ребер сечения. В многопустотных плитах высотой менее 300 мм допускается поперечную арматуру не устанавливать, если она не требуется по расчету.
По образованию или раскрытию трещин, а также по прогибам плиту рассчитывают в зависимости от категории требований трещиностойкости.
При расчете прогибов сечение панелей с пустотами приводят к эквивалентному двутавровому сечению. Для панелей с круглыми пустотами эквивалентное двутавровое сечение находят из условия, что площадь круглого отверстия диаметром d равна площади квадратного отверстия со стороной 0,9d.
Полка плиты работает на местный изгиб как частично защемленная на опорах пролетом Lo, равным расстоянию в свету между ребрами. В ребристых плитах ребрами вниз защемление полки создают заливкой бетоном швов, препятствующей повороту ребра (рис. 11.7, а). Изгибающий момент:
.
Армирование плит. Применяют сварные сетки, и каркасы из обыкновенной арматурной проволоки и горячекатаной арматуры периодического профиля (рис. 11.8). В качестве напрягаемой продольной арматуры применяют стержневую арматуру классов А-IV, А-V, Ат-IVc, Ат-V, высокопрочную проволоку и канаты. Армировать можно без предварительного напряжения арматуры, если пролет панели меньше 6 м.
Продольную рабочую арматуру располагают по всей ширине нижней полки сечения пустотных панелей и в ребрах ребристых панелей.
Поперечные стержни объединяют с продольной монтажной или рабочей ненапрягаемой арматурой в плоские сварные каркасы, которые размещают в ребрах плит. Плоские сварные каркасы в круглопустотных плитах размещают только на приопорных участках через одно два ребра.
плиты из тяжелого и легкого бетонов армируют продольной напрягаемой арматурой и сварными сетками. По четырем углам плит закладывают монтажные пет- ли. В местах установки петель сплошные панели армируют дополнительными верхними сетками. Пример армирования ребристой панели перекрытия промышленного здания приведен на рис. 11.9. Номинальная ширина такой панели — 1,5 м. Применяют также плиты шириной 3 м.
Монтажные соединения плит всех типов выполняют сваркой стальных закладных деталей и заполнением бетоном швов между плитами (рис. 11.10,а). В продольных боковых гранях плит предусматривают впадины, предназначенные для образования (после замоноличивания швов) прерывистых шпонок, обеспечивающих совместную работу плит на сдвиг в вертикальном и горизонтальном направлениях. При таком соединении сборных элементов перекрытия представляют собой жесткие горизонтальные диафрагмы.
20 Конструирование и расчет неразрезного ригеля методом предельного равновесия с перераспределением усилий. Конструктивные требования по армированию.
Расчет неразрезного ригеля. Ригель многопролетного перекрытия представляет собой элемент рамной конструкции. При свободном опирании концов ригеля на наружные стены и равных пролетах его рассчитывают как неразрезную балку. При этом возможен учет образования пластических шарниров, приводящих к перераспределению и выравниванию изгибающих моментов между отдельными сечениями.
Сущность расчета статически неопределимых железобетонных конструкций с учетом перераспределения усилий заключается в следующем. При некотором значении нагрузки напряжения в растянутой арматуре из мягкой стали достигают предела текучести. С развитием в арматуре пластических деформаций (текучести) в железобетонной конструкции возникает участок больших местных деформаций, называемый пластическим шарниром. В статически определимой конструкции, например в свободно лежащей балке (рис. 11.11, а), с появлением пластического шарнира под влиянием взаимного поворота частей балки и развивающегося значительного прогиба высота сжатой зоны сокращается, в результате чего достигается напряжение в сжатой зоне , наступает разрушение.
Иначе ведет себя статически неопределимая конструкция (рис. 11.11, б). В балке, защемленной на опорах, с появлением пластического шарнира повороту частей балки, развитию прогиба системы и увеличению напряжений в сжатой зоне препятствуют лишние связи (защемления на опорах); возникает стадия II-а, при которой , но . Поэтому при дальнейшем увеличении нагрузки разрушение в пластическом шарнире не произойдет до тех пор, пока не появятся новые пластические шарниры и не выключатся лишние связи. В статически неопределимой системе возникновение пластического шарнира равносильно выключению лишней связи и снижению на одну степень статической неопределимости системы. Для рассмотренной балки с двумя защемленными концами возникновение первого пластического шарнира превращает ее в систему, один раз статически неопределимую; потеря геометрической неизменяемости может наступить лишь с образованием трех пластических шарниров — на обеих опорах и в пролете,
В общем случае потеря геометрической неизменяемости системы с n лишними связями наступает с образованием n+1 пластических шарниров.
В статически неопределимой конструкции после появления пластического шарнира при дальнейшем увеличении нагрузки происходит перераспределение изгибающих моментов между отдельными сечениями. При этом деформации в пластическом шарнире нарастают, но значение изгибающего момента остается прежним:
.
Плечо внутренней пары сил zb после образования пластического шарнира при дальнейшем росте нагрузки увеличивается незначительно и практически принимается постоянным.
Расчет и конструирование статически неопределимых железобетонных конструкций по выравненным моментам дает возможность облегчить армирование сечений, что особенно важно для монтажных стыков на опорах сборных конструкций, а также позволяет стандартизировать и осуществить в необходимых случаях одинаковое армирование сварными сетками и каркасами тех зон, где при расчете по упругой схеме возникают различные по значению изгибающие моменты. При временных нагрузках и разных загруженйях расчет по выравне?
