Расчет лопатки на растяжение

Расчет на прочность рабочей лопатки последней ступени ЦСД турбины

Из расчета последней ступени ЦСД, мы определили и выбрали следующую марку профиля рабочей лопатки [2,стр.88]: Р-35-25А.

1. Расчет лопатки на растяжение:

1.1. Определим напряжение в корневом сечении, без учета бандажа:

ρ = 7,85*103 — плотность стали, принимаем по [6, ст.124];

U= 216,66 м/с — из расчета ступени;

μп = 0,2 -отношение площадей сечения профиля рабочей лопатки;

dср = 1,38 м — из расчета последней ступени ЦСД;

lлоп = 0,4218 м — из расчета последней ступени ЦСД;

— напряжение в корневом сечении равно:

1.2. Сравним величину напряжения корневого сечения при растяжении с приделом текучести стали, используемой в рабочей лопатке:

[G] = 370 МПа, -предел текучести для стали, при температуре до 500

кзап > 1,7; полученное значение коэффициента запаса по прочности допустимо, следовательно напряжение в корневом сечение имеет необходимый запас по прочности в 2,718.

2. Расчет рабочей лопатки на изгиб:

2.1. Определим момент сопротивления:

Wатлас = 0,168*10-6 м3 — момент инерции для профиля лопатки по [7, ст.67];

в = 88 мм — хорда профиля рабочей лопатки, из расчета последней ступени;

ватлас = 25,41 мм — хорда профиля по [2,стр.88], [7, ст.67];

2.2. Определим равнодействующую осевого и окружного усилия:

— Окружная составляющая усилия:

D = 249,273 кг/с — из расчета проточной части;

ε = 1- степень парциальности, из расчета проточной части;

Z2 = 82 шт. -количество рабочих лопаток, в диафрагме, последней ступени ЦСД;

С1 = 426,861 м/с — из расчета проточной части;

С2 = 132,391 м/с — из расчета проточной части;

α1 = 18 град.;

α2 = 88,046 град.;

— Осевая составляющая усилия:

Р1 = 0,23 МПа — из расчета проточной части;

Р2 = 0,22 МПа — из расчета проточной части;

t2 = tˊ2*В2 = 0,6*0,088 = 0,0528 -шаг установки лопаток на диафрагме;

— Равнодействующую осевого и окружного усилия равна:

2.3. Определим изгибающий момент:

2.4. Определим напряжение изгиба в корневом сечении:

GДОП = 35 МПа- допустимое изгибающее напряжение рабочей лопатки;

Получившееся значение изгибающего напряжения меньше допустимого значения, расчет оставляем без изменения.

3. Расчет рабочей лопатки последней ступени ЦСД на вибрацию:

3.1. Определим для 3х диаметров статическую частоту колебания:

— Определим площади сечений лопатки:

fк = 0,003318 м2;

fср = 0,00116 м2 ;

fп = 0,001943 м2;

— Определим момент инерции:

fатлас = 0,000162 м2- определяем по [7, ст.67];

Iатлас = 1,31*10-9 м4 — определяем по [7, ст.67];

— статическая частота равна:

Е = 19*1010 — модуль упругости;

3.2.Определим значение поправки на уточнение профиля лопатки:

3.3. Определим значение поправки на вращение:

n = 3000 об/мин (50 с-1)

— уточняющий коэффициент:

— поправка на вращение:

3.4. Определим частоту колебаний вращающейся лопатки:

3.5. Определим резонансное число оборотов:

i = 1,2,3,4,5 — тоны колебаний лопатки;

— для корневого сечения:

Как видно, из полученных значений резонансной частоты, турбина «перескакивает» резонансную частоту при наборе номинальной нагрузке, либо не достигает её. Номинальная частота вращения ротора турбины составляет 3000 об/мин.

3.6. Определим запас по резонансной частоте для каждого тона колебаний:

— для корневого сечения:

Запас по резонансной частоте составил 6% и выше, можно сделать вывод — что работа турбины на всем возможном интервале нагрузок (вызванных различными факторами: конец топливного цикла, пик энергопотребления, и т.п.) не вызовет резонанса и тем самым разрушения элементов турбины.

Источник

2.2 Расчет пера лопатки на растяжение

Центробежную силу профильной части лопатки (рис. 2.2.1) с постоянным по высоте профилем определяют по формуле:

,

где — плотность материала лопатки; Fл — площадь поперечного сечения лопатки; l — длина лопатки; r — средний радиус облопачивания, на котором лежит центр тяжести лопатки;

-угловая скорость вращения.

Схема к расчету лопатки на растяжение

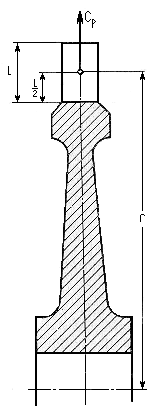
Рис .2.2.1

Напряжение растяжения от центробежной силы, развиваемой массой лопатки в корневом сечении равно:

Как видно из формулы, напряжения растяжения лопатки постоянного профиля пропорциональны квадрату частоты вращения, длине, среднему радиусу и не зависят от площади сечения лопатки.

В том случае, когда лопатки скреплены в пакеты ленточными бандажами, в корневом сечении, помимо центробежной силы собственной массы лопатки, действуют центробежные силы бандажей.

Центробежная сила ленточного бандажа определяется следующим образом:

Тогда суммарное напряжение растяжения в корневом сечении лопатки равно:

2.3. Расчет лопатки на изгиб от парового усилия

Действие пара на лопатку обуславливает возникновение силы, которая может быть разложена на окружную составляющую Pu и осевую Pa. Обе силы относятся к массе, проходящей через лопаточный канал. Pu может быть определена из уравнения количества движения:

,

где G- массовый расход пара через ступень, кг/с; e — степень парциальности; — число рабочих лопаток; с1u- проекция абсолютной скорости выхода пара из сопел на направление окружной скорости, м/с; с2u- проекция абсолютной скорости выхода пара из рабочих лопаток на направление окружной скорости, м/с.

При угле скорость с2u является отрицательной, и в этом случае в формуле знак минус меняется на плюс.

Осевая составляющая парового усилия обуславливается как динамическим действием рабочей среды при обтекании лопатки, так и разностью статических давлений по обе стороны лопатки:

,

где с1а и с2а — осевые составляющие скоростей (см. рис. 2.3.1), м/с; P1 и P2 — давление перед и за рабочей решеткой, Па; t2 — шаг лопаток, м; l- высота лопатки, м.

Треугольники скоростей турбинной ступени

Р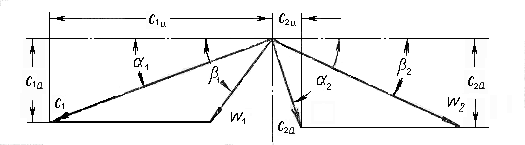 ис. 2.3.1

При подсчете сил по приведенным выше формулам необходимо выбирать режим работы турбины, при котором окружное усилие достигает максимальной величины. Для большинства ступеней турбины, и в особенности для последней ступени, таким режимом является максимальная нагрузка турбины: для первой ступени паровой турбины с сопловым парораспределением опасным режимом служит нагрузка, соответствующая полному открытию первого регулирующего клапана (остальные клапаны закрыты), когда ступень работает с большим тепловым перепадом и малой парциальностью.

Равнодействующая сил Puи Pa (рис. 2.3.2) равна их геометрической сумме:

.

Силы, изгибающие лопатку

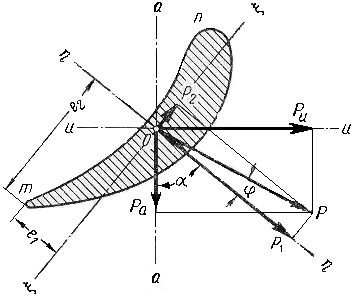
Рис. 2.3.2

Для определения напряжений изгиба необходимо найти положение главных центральных осей инерции сечения и , проходящих через центр тяжести профиля О. Силы, действующие в плоскостях наименьшей (ось ) и наибольшей (ось ) жесткости профиля, обозначенные соответственно P1 и P2, находятся следующим образом:

,

где — угол между направлением силы Р и перпендикуляром к оси минимального момента инерции.

Данная методика довольно сложна, поэтому для расчетов применяются следующие упрощения:

1. ось минимального момента инерции без большой погрешности может быть принята параллельной хорде профиля mn (рис. 2.3.2);

2. направление силы Р может быть принято совпадающим с осью , так как угол между ними обычно невелик и

Таким образом, определив по формуле изгибающий момент от газовых сил, можно найти максимальное напряжение изгиба в обеих кромках корневого сечения:

и в спинке:

В этих формулах через Imin обозначен момент инерции сечения профиля относительно оси , а через Wкр и Wсп -минимальные моменты сопротивления соответственно кромки и спинки сечения лопатки относительно той же оси. Напряжениями в кромках, вызванными моментом от проекции силы Р на ось , т.е. силой Р2, можно пренебречь.

На лопатку, изогнутую силами пара, действует центробежная сила ее массы, которая стремится выпрямить лопатку и поэтому создает момент, обратный моменту сил пара. С учетом этого влияния центробежной силы результирующий изгибающий момент равен не величине М, а М, где — так называемый коэффициент разгрузки, меньший единицы. В данной работе расчет коэффициента разгрузки отсутствует.

Результаты расчета пера лопатки на растяжение от центробежных сил и на изгиб от паровых сил сведены в табл. 2.3.1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Источник