Расчеты на прочность при растяжении и сжатии примеры задач
Содержание статьи
ÞLtN
qYäBÜÒí|(XÊ=!,?Mk¶82!t’lâ¶5V·²(O9jÉÓ
ðåôº]¹aqÉ(1rªä¶¥Ñ+R+9â{n)²ç,NÝ{ÓÎí¶{Ú!¸íú&(OMP0£WÞc4ÝKKmÞ÷ ØƲ8uøFÁØTwwÍ4PåAj¨gl[*îÜÉÔ¹©¤àwznç nÇZ³4ï12ÅÿÁ3 SWN+=
AµÏ¦ù¨rñú*n¦fÃlnм&r/r©ÒTê:´zçIg f§rySÏ0NébuÉÒ)]e J§t^Q×)]tqeë.Àb±:(;KJþ>ÃCÙ¨ÓuaZÐVd#èt]fÚlßźªÈFÐñ]Fvlë:SÙÙ:®k1[DJÇumv:xJ,*L²#Û`´IÖqd^x
G¶x|ý¼ÙVèkMC±
5E·ê*W-ÅÈ·÷²cK]Ï{¿*î¬Ä|
ËÊà;¹ûí«æðxð’B-å
P NY»å®õZo¦(µæbäµX+^úvÜM%¹æyóL÷zóê_,~ÒFÁ»JV²^ØßþêèvéHªCÄs{1t}8OÇõò¥Nüu)_¨
endstream
endobj
5 0 obj
>
endobj
6 0 obj
[ 7 0 R]
endobj
7 0 obj
>
endobj
8 0 obj
>
endobj
9 0 obj
>
endobj
10 0 obj
>
endobj
11 0 obj
>
endobj
12 0 obj
>
endobj
13 0 obj
>
endobj
14 0 obj
>
endobj
15 0 obj
[ 16 0 R]
endobj
16 0 obj
>
endobj
17 0 obj
>
endobj
18 0 obj
>
endobj
19 0 obj
>
endobj
20 0 obj
>
endobj
21 0 obj
>
endobj
22 0 obj
[ 23 0 R]
endobj
23 0 obj
>
endobj
24 0 obj
>
endobj
25 0 obj
>
endobj
26 0 obj
>/ExtGState>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/MediaBox[ 0 0 595.32 841.92] /Contents 27 0 R/Group>/Tabs/S/StructParents 4>>
endobj
27 0 obj
>
stream
xZIo%·¾Ðè£àQ ëfû 59Ør&Ê!ÿ>,îìnö#¶a·^w³XËW«_Þ?|ùð>=>>Þß_>üëõ×éÇç·?~~xþ߯߿|úüûËûç·ß~øï/ïxëo¯/¿¾~Ùï§ãù4ooÄÄøôüñöMÔýË&n(9i+vO~s/}ó7Ó§ÿÜÞÐéSøiãÏono~¼ã÷?OÏßÞÞA$( Jg(Ñî!¡»03}ù´róêTQý÷íÍ?ZÚÜ2OÛ0bmÇê2″ÒíË5ùU¶ò@ åøTM_^oo>þe)©I+CXõµ´gº|w:v¬HZm>ÎË~Çño :3³×î¢öÓ~’ðÊü-
òðÄî[cy(.öeàÍÆw?ÝÑ{¸Ó÷;q÷Óýô×éq§g~f·dMc꾫 ýwªc]h¡K4ø¨ú¹CgÑþrùD¹¦ÁòioÜEéýºhÏæDDvÿÐÕÌ-Ó³ÕôÈÆÈ51¼^»ÐÿºØh}1çÇ$¿ì%þäþÉC¯¹ èÿ3-uküU3OÑ¿qÄM«ù©[äaì´ÃX½1îqÞ3ÿt4Ç]üz¦9úä©AàseüÏbΰ,DoòCð$IDqÚ[Ïf@CU·çF+F @àlZ¯¼*[{mã^ô}ÇEl=ä;Ðøêúrïh/>Û®ã²
âó
Q±*ÌëY2ú4kÜmåßÒaÖTÎËÁªÞz[ rÒ{JÐ5BQ]
I:R¤ÙR)(é[zwÖwâ]ïʱ ªG¿kë®ÔÇ6ÖÊÊ-åSC»Ü
w¸ïÑ
ð¥ (;g§Nï;W
qyÆ»¡`’-½Üí¢kT©¤Å=£5æ..:,½ÜjÊ&BjJï×Üqxã²ÂãФWËôºXßâi0KHª¨-Êqå3e´#ItgÊÙO!`:Ý&-feõ¢½U!j´Bl¨ÒÈIÒï!¤_§§ì£¡ã»QÁ:,òêµã5irÀÜÕ-ÔÖâ.Ï?Hì]ö¯N®à¹ëb·!ÂÁ4¥ÍFmZ¹©ÄFÊ1´ C¥m¥Ä¢vfYà)9Ø+å3PÑÉSÈǹÚY{tL.LÇ]’gßIuá ÆCξVïR>Á
£Ô¦k((çe²8yR#êÖ®¦
-Du®-¦^R8{)¼À{¼¢#,*mKk¸um5õÚÑB8µ ±sÈyé˧:»úpk»r)e26Z»ÀÂåPÚ¯®>â_§a
ɯ*êÃJ&åQ LolǾ6ëwAÍXa¬¨JXâÖ¢F¶ì*`QWé7URTc«;@ÄgÒúw>øÆB!ùÄ}mFBlgÎö, V¼º R kêä
1¯á¦H²i
ÏÉ7dT³`ÇVX¤jkË:˧åñjX=äj¢JØuV>Æ26Haif
²Sè9ºläJ³5¨qMàܲÇÝÏ¡Ö>Ë_K=RKÂE!rô¡-lVæ¼ø:æH;Yb¡N¿ç5F9>äf|wUÅPIb!æül»ë*1®JCãhÇâ¨.!üSôåÚPqPT¤|ÎX¬ÐMO }ç
jSÅw¥käÌMdåîÜ^¹kêÈàî]2#°r°gUFµ}©_
$Áu¦Û¹9*ÍbÐÒ¹îYS!)õkIßaOÕKÕÌ¥L9çqS^WÛ
¸WQQmY2Oé)ÆÚX±³KJ AÔÖ~¡iVkµ´êêq¥±¥ñ¦ÚA×(¨|:X$§5.%S8?fÖ¼7¸Ô¢r¨¿$V}^lçä%ûGå¬eªÒ|¿Ëi]Çs뼶BfÅ{z!±¬§Î˱d(a
ÃýeIädÖ¥SR¶¶¼ûäÎÖâÇz£¬µ7q®sTV^ÝK£ûÐ!Â$)R¾} ¹»F·iïT%jÅxÐKöWWK/&ñL½Þo»h´×FNඥh´µÃ¹Ø¥9C÷p
fT91,d®ÄfæVW϶_&éT[q³æåÑo.ØÒµ¸.YÏwrvè½n ]0V.
#|qçXXU´ÓîÄ)dà¬UØK_ÙrQ+5>!EÆ÷ZÂd[YRص p¼Úfìä
}pãcBðÞ6¼¤ñIÉiÿµµ4fÐcZÌÚôRB²WTEÍÄ¥máóÜ¥cÕ&düè}Ýë`²Ú1½ÀJ6Ú½2¨¼>ä]#hCT)GÁ¬©²8RK6¥OÐäÁU¶!×-Àâ%Õ¼4ü¨ïAbô©6Ϊ/6£ëQÇ*ÆÚ¤cnö«Ztø@f#ª ã©Çø¼5Ô!
èÆÚ8aqèSkÿE×fÏÉ9t»ÁøP²[å%*a¨À§16FEö©k°A¡¢6¨aÊÆAÛ1K
*`³´Ý «Ý|¬@7¨0uÊvelÄ7°Ë]+C6âØué;ô*ØåR>d#¾].4akÇlK*Øåâ8Êv9
ÁI2ßÀ.3&Íìüi°»ñû¹ÿ«wL-:Y½ÓòyÉô«0ÍǦòbÃSGC½bÃSP»l)6*¨!|ʧ¸øsQÝX};s°
kNbvù;Ñù½x³zÇfaî¯Î6ñøR, ¿øÝLgø|¹TU3m8ãÉ»ðeUg~Nepâå§];Æ]aεü¢iõSfð[¶®]Ê5&_Ø!£¸äÌYïÕ:çË
q@l/ê~¢¼ëC½GÃ2ÖðeV
aHël)Ë7u8Á0À¦ÌÌ!
üRª+àÒ )Aú/t¹!OÚÙÓòâÇÊWúúÕÿ¢Òu
endstream
endobj
28 0 obj
>
endobj
29 0 obj
>
endobj
30 0 obj
>/ExtGState>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/MediaBox[ 0 0 595.32 841.92] /Contents 31 0 R/Group>/Tabs/S/StructParents 9>>
endobj
31 0 obj
>
stream
xí[ËnÜ6Ýð?p0ï`àg@¤1ÐE
8nSwºèß+»3N²(c4¢ÈsHçWwVgOoßoÐééêl³¹}ÿçÝôvuóðõÝêæ߯w«W·÷¾Ün>=|Y½ùç?õóÝí»Çõ_^ óã£Õ5G¡ÇG÷G³+´X»Ïî¢Þ0îÿ>>»è>~µðõ§ã£·Ïøówèæ×ã£+× o´k²ÕÁÚb©pÔ Çû¿
VQÒê_ÇG¯Çm3KCÛbÛ~û©,_6?K«GX7H0_ªÐãÝñÑÇs¤¤ÂJ ¦Ð_?^0JÓþ «h¹çÍÃçü¼~xØnå7XÌô4F«WòåÅ/¦FT`»¶f
ÂÄ»-¦Ðð©C¼$LI÷yæþ/üñZ¸»yíõZ¹CÅü×õøÞ¬®
¢[5áÚb-G0#þæty2[¿%n8hMslf@»6ÀWI1WH¹á·1FÊÕ`a¾üþ}q&HÆ5M¨éж«öýÜx¿eX;°{îù~Ê6@c×Ã0h·x7+WeiÄ0¾¦,CUa)fXºcuM&¡q6¯O¸ûÔ¼’ìâ¿_®©ôÓTÄI¬(|êu8ÍÂ¥LÛp9üû»Bi8§ýYQwv}»¡Òíᬧ;s:iª¿¢¥
8;mc VÓméÅáïÐƤ©ô~n/¸æòܹ¬´rÍÀÃU½’á-üº`Û/l§§v.lê«ÚóôUÉNGæcù3
·E^©p ¦Î¡çήTf ÔDè}MÖÉðvÕ¢ÐêxrJßÑ)}Qú8QêBO¥>Ò;OsAêS^êmzu¥¾Óm¥ÜÛX[CL(7″¢eb.gñQH³µf|ÅÙÎÒSxº}ðÇîCzî.3GÚX£ÿônÞ»Û²:Ó
ǹ óp!ü??1ϱ?çÂ(ûëκ#Bp¬E¡#øÁµôòT·,;¥ë2*õÒº4S¥4AEwP(Pêç.>õV:Nÿ³5ÒQ§Ã æfñ.ÎòëGzkÓW¦Y¿í»©ýIù-Õ¨|b]R9″rØ£)3SÃn{WR5n!û¨7/iݺÎ3ÞÕæb¼°úmJ~$(¸WZæ.ÙeݦԻ׹³kýk°³ðpI¢9¨â17`7Æ)í;§X¦Íÿ÷A,*`Î(ÞCnÜO#ññeÇÞMIÜ8%»Èxä3;ápØ$WÇâô¤ûÞ8,-éÃH¶´qjFÓ¥èÇÖï´N9©LvÓÝh(ÄÛéD¯j¡tC
Oç»{ãz
Ny,¨f+HôèäÇõèÆ.G§]¬ñèf´àÑ£»öM÷¶Ä»iï9áEÿlÿý3ß R=õÏ¡nËKÁD¬ü3û»±Wt6^²¼±·þ¹¤îKþéöÑØðÿÊbkëü{,ÙãêÜ1Ûþªòæ ´ ëîÁp.¿Fç )HÉAa,]nv,ìÄAhsZP®·P³Ð*»KÉ{h;
èòÃhs;MúXá¢{ÀEMoÜ7µÑfæ0÷}Ô^÷¡Í(`¤#¢Ñ021R`Ú!NDkq6ÛÎ’LùØÃó[õEã$n]Ú9ãÚ¢P¦»ôËèÄ}UÛúånTxùq+²,eV¤ÙåÒÕ^òsHæÉ~>ó²4óÇ]®M$Ïâ׫x¥ÏÒtÈÎñ
È[vb¶gHÒñ¥v¨¨Îc[¤DXLÎÜåìBòauåÿYµY5³tÉYÃL¥¤3¤l,qÍ#O%mp&Ú2ì»ØòÇ~hQ¥+,&ó«0ÛzªêÖ0ÓÚ`Y±19Ñ[ ÙbcÆúdßR¥ó¨¡tK/§JÃp¡×4¥¿Þºê’oc&Ѿ¦ÿßå÷ÖÌðfRû$ÉV·V@Z
ë½Mcj¢Õ@´5èR¢ÕÙY3ZÔêJKÝÅ£´löÓÛbê6±>xP’Ö@³»¡ZGÍÑƤOByµO¨ÖEW3óÙí4,£d4ò!¥véw»#
ì¢KåC$-inîIc0£Z·ÓW%ñmñÅÖoE³õL#0Ð$êMCoFõµÑïUIö·ÆTñº_×ò.n~Í7MÇtòóêX¬ÄÚ¥ìvC¹T3ËÆzz>I³k@nA|-ÀµÂõÍäJý%Û ÚïÔ²åÔ08ð?â/»
endstream
endobj
32 0 obj
>
endobj
33 0 obj
[ 34 0 R]
endobj
34 0 obj
>
endobj
35 0 obj
>
endobj
36 0 obj
>
endobj
37 0 obj
>
endobj
38 0 obj
>
endobj
39 0 obj
>/ExtGState>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/MediaBox[ 0 0 595.32 841.92] /Contents 40 0 R/Group>/Tabs/S/StructParents 10>>
endobj
40 0 obj
>
stream
xí]K·¾Ðèã*ÈôòÍ& °3»b ä ø زâ¥ÄÙòïÃG,6ÙÝÞ9$@lH;ÛÓÍz²ê«»ºøåù§?|ÿ§w¯_Ý_ø@ÙðîÇׯè@ìÿt`FJÚÈQÛo~¶7ýæ[6
þùú>
_
üúׯÞß7ß
ï~ÿúÕÐ
GâÌF»£¶_SaÐiøåSãâü¨õ¯_}SÍõcOt4aì÷wL-2ÂG¥ËñðM¶1
a4æ¾UÃ/_¿úñW-¦¤´F
ò:}jy§¯ÏÃýO_¿ü¼lÊË/Ï
)K&ø4¤ðpÿGGòëóïR¸VD^a¬üN6ÉF>
ßZ
ÐãÙòÁþy:
ø¨ôQÚÁ·B?¶mCl;p7
̱
c¨’Áþ30BôbƸ.%½]HÁí!=p[Úyæp«l_IÀ¸+ 0©Þ©É§iÕÙ6Ë(RyÁÇó $µå
Ù¨&Á
˲ÔÑRéè)øMäpcçD ñ;¨ð]e wLñŨ 5v !_£Èd÷Wèà×WLÂùìܸçÀ&N~ÇæcÕ&@õµl¾¬íVÂ¥GT.ÄÑc7ªYãñ³ÍYÍ}~4ªÍ¥Ô#¥_âLñ|BD ã@J塯¼,.Å9)ºaQF Kø Jgp5å»?Âå8c?5kñ%r¨dÄ*þi=¡Iç8Ü%Ðó>A ¶¤
L2!ÖÕÙ£¢Ã×=]FqZz¨¾xðW²³µ½©©/Å4ª¤Ã?³Ûm~ÂJ]0øô×xd)6 Ð¥îZºK©7
àÖÊ_*T,ü%yÚÄ^ª¸ ËÔãìÌWDtÒÃi§S¶ÖÁcdß²«3m³*TµyUª»j=MÜ8¤WÀ
Âprî
HTh;MY,!,´BÔÀ©ÑÔ(z¹(0·U4õÕ»!
ACè«CçX$D_öÉ.Ó ¡k[àn¬L×Loböäjç=K.[¼M9U 3/HsüÀ ü7é¸Lb0Sæ.Tö¡QåjáÁsY6åSIÚ-IG!çã¦>BÊ2©rè¢$`’ÓÂ%7ÞTôÄ!(ÀÂD;§z>ê9Á~
Þw.{ÐS%«è&½0«õ)Ò®O]¶l¥)ëS-¦{b6¯¯¨¤êaCVØ §¨hÐXn*DàPzì)Rðγù è@ceUhSL³ÐPà×¢J~¥ô »¤88oKÒ¥r¡öPø´Ì1´à¥YÆ-‘¥èÃÐƸÕZdÍ:k«1ÙªQèAd/:DÌÔQ
Ç0)+Í ÒÏ)Pij{óyø*¬Å àÖ5lÈÂï«cYjõüãõ+ʸ¸Eúd¸«ríoþo·¶þ_
í½H
´X>j£²ztPpMÝÓI׾YjÅ|4Ú@ee4Ë(9Å_òØÃulUp¥^Ô#âE#çßÊaåXIë$W]E&ÿÆïè×}k²r&+ß:ÇAÞ
ØEnBKWéÆápE¬¸°l.#(·Ïd&bAã¸n_LÆýpkÓ@ßÿáÃçOÃÝÇÏ?û&Ï ?û¸n/LÊ?Ù~*Ù®ÛtCòƾªµ¼¹%ù©þ«mq@É>lÄ/sc®UǵiÆ2Üç©LÐÛéA0õÖÃp¨ê-NØ^Nfê~3RÇû;¹EßPBº®ÚUÎHÅ.ú-/Ä4:Aùäd14¶ÁÜë6¥vugHðÉä¨P^ÓB@£ubwRyg7;×îéÿùÄ®RøÎ 0¯uÎjÇ»uè±¹Ém2ng VäÜÜ/§a¸«d
hbÈÿçÆDúÐf.Ø*úØKÉ¢.KJסÂKèÃÐUÛ5Ы|,ÏÕ-ô¸Î¦Áõ*úÀlo¡Ú»éüXQ[M¿?öÓ*ù¿²×7X`
üÑÃÂþÌív¾°þØ«?fa¡°þèã¤?²:¶ñkàÝZ üq7²þè ¿?æyô:üÁø£Ï5ñG_PÔm{ ¬°
øgùn B[ÿ_ ЩN;1¦bmØsÛ¦BÚ×Ò:ÒûFZßM Ò:¦tUZï!¼ÖK7Ò:L¼Î6ò:°½?¯c¾·ò:«óú~ú×WôVÓ¯óúèOü_
ä×̹Ë#¼Îî]TÙ3TÙ+²;¯³ûnmÀÌÈÚú;¯{‘#3m¸±ÛyÛ÷ë@J-®ñH^çöúÍÜîvÖ9Ê,)9¬¹t%LGçuïôÎÖn¦Éåu7¥ÒN-ÜaXlò:Á»gõÞ¥¦{:%xó¯vë0OaíËoc q$/¸µÖÏù¥´.-PÚ÷?¤ûyúWÁ¬OqÏo±L®¼MÉa¹ÔMòë/yrRnÛYÜË|/5ë£Ü,PÛê?ômgqéÖª±ÿtdñàçK×32pºÞòcsVGnÿËÙÛñ+R%@$©,
µv£â¡FÇéåT&·$TPIÉX¾3¨Y°¨WeªcÆEKƪ æVÈ+¥eè¨3ÞaåwBP.¤MÍ°G#í ]e°®ù»7¯jxÝ$ÆòÅW@3/±z¦¹lºÐzôÚ1¶ç´PìbõD&WüDãÖn»9¿DDØ|{¡óSïfB-ÕTÔ¬§ÃE5ÕòmÔ×KZ¼®R«ôVÛûÅÕEe9ê[Ç8&å¾Zú»eødúîÍkJ]ûóºS/²-9)fâQ7*°³ vßÌqðµ·ûYþ*,øVf úÀ6Údü³»Á®Û¼±îc ©3öߢý¨Õ[r^÷VÖ«vòépÚ,M!n¢£°7&¦S~7¡ÕÝÚÏbûØé:ÉÅ®ð¹u+·ÌÛ»kXMwrÝ’ÿ|?»OkHx’KÌbGä
Ð]ïf¦_ G/Þ±U-º{ÑÃFÆ2·ñs°ÙAu£|ó-éðÚüL~×3öËÒ2ÄR
Ï$±Qh{=¼Ó±ÁhÝêèÓÓ¼Éc¹t1arAG|KGuCc¯»N;k&ª#¼3ïY°U?Ã?Ëö.XPíwÐÞºqà$½57
ÒQAgÒz!¶XyåDËOÅÒHzÝbq;Øåîk!§ú0¿Á{)ìÔ:ÚÕHí®
*¦ôn5í]¿Q0µÖ¦qÚÉ]Lóí(»ÐÕø
Ü|ch^PmùætÇíÇØoö^6N¦°,&-¢½ÂÒ(ù«¼vU_ìZÛÚËWÚÁRí`YDÁy·ÅúÏúºò
GÂí:_§*¨WÜ:¡
SAÐB´NjK«bÒÚm/¢bF¢K*®¨»5Akët~}{*T
²=W¯!W× âñr’Úµ±^wÉå%[Ùss5½9.hå©k7 hEa¡·û¹ÞQ³ÅÅ+è5{;:³ÈÁ¢pþN~«
°çäÖÂKê_ë3hË«z © {VìÆ;ÂõàÿlçÈv ÅìT6¾µíQLDD»
£÷]íEÑ/ó*f¹
EûÚ7¾7Ǥ6t/ÞjÿËQtYÚ(ÚÆGZØeEï¥dQ´Ô%¥Û¢è9MåLÛ(ZÎ÷±_¢sÐÝÑr¾½¨¤¿D3ÞD¢¡¸J ÑÊÞK’hLgDï¦ SQÛ ºÜ¶·ë~½[0ÀÐY°>ÝG¯¡dkzÐÀ2Þ1@Ð3m»èzkº/EÐ{
z%vÔ²JÔÈ2¹éÿ¨xðd:Ä
QK:®VÀdæRÊ#m/ñ¨ÖÁ*é88càsS+ÖYp1&»åÛr¨c §!¥¿tb4>ó.`ØÏËñS8v5¹÷18’~Ãà>ÑáÍÛÇfMl¤D´n8|ªç°m1
ågßÑçZúCÓÑãï’©q×Mq½×[>zìÈ«y[âÓPOé#)6ßØyÂ#£þÌðÆYq¡Ìÿ«
v~r6h=¹2øýýãþéÿ j¨h
endstream
endobj
41 0 obj
>
endobj
42 0 obj
[ 43 0 R]
endobj
43 0 obj
>
endobj
44 0 obj
>
endobj
45 0 obj
>
endobj
46 0 obj
>
endobj
47 0 obj
>
endobj
48 0 obj
>
endobj
49 0 obj
>
endobj
50 0 obj
>
endobj
51 0 obj
[ 52 0 R]
endobj
52 0 obj
>
endobj
53 0 obj
>
endobj
54 0 obj
>
endobj
55 0 obj
>/ExtGState>/ProcSet[/PDF/Text/ImageB/ImageC/ImageI] >>/MediaBox[ 0 0 595.32 841.92] /Contents 56 0 R/Group>/Tabs/S/StructParents 11>>
endobj
56 0 obj
>
stream
x[K·¾/°ÿaë ËåM@`N8pbÝ6>(²¤ø`ÉQ6üû,]E²{z@f¶,ëùUótøúòóÇwï_voÞ^^Þ½ÿÇvÏOo¿üúãÓÛÿüúáéûw~þüîåç/~ø÷ß_â£?|x÷Ó¯ûýîx>íoïï®j’äîíÇû;±ãáØI¯5;ç
sáÍ/aз?Èi÷é_÷w|÷ þôùÏoïïÌ7?îÞþéþîF¢
⼡Ä/WB1í¾~J[zhOy ýü í»#YGcòC¶ê
iĸoíîëû»¿1e,³zçìÄDÞoWR¿Ýå»ÓîiAÇ///_~YVåõË¢JÊì-¼{ú>.ùÝéç’&awÂ0oUxÉlÜÖLeÂo@ü^{ÿåþQÆï>Í5>ß»L¶l©9Óº+ÂJfȲÅå=k¶íªÉGv23îà
;6Ĺ
½CÃ?/ñ{«61.b_æ¼SجaCj9V¯Ç¸z ¤%Ä×ù-¿q=â×ß
nVùuU¦¿ ne£ðý¾n ÙöÇÇl̪}3vë¦!vUÎ$×,5ÌÙÀ¬ôh¦vOÕDb92hó0½’û®ØÙÓȾ¬ïÖ»>ej&IÌÙôqòX^§´¾Ï~¦Knf)¤ª)²ÐÔ,vÞd
3/0ðo§NçÇì$v§fy:Æ’%!Ðw÷ÈÏy¦·m5ñàtVX¦&b)Ê;Ï¢ÆÂGb0 Éè#ô7èŲصgG®£QAGåüÀ¤¸Ç¢¢úó^(,ª0´§3x Ç!*æÂ)Q5ÅÌM2″dæXâƦ(ÄR.nîægïÁCÌãëÆ¢%d[¦UÞöÆÓ§8Ì¥,÷, nøq
×d+ú¾’Î9gågP¿Föz¨ZCôÉkusñõd H2#% ª,bÿ(´ßÎ*~ܦø-nà¤Ã7¿m|fÊ[¿MüMúÇéøí»ó[qiãE`kÐE´Úc¶Öwª[@ÝQ3Y¢K-Â&Ú
Источник
1 Растяжение и сжатие | ГОТОВЫЕ РЕШЕНИЯ ЗАДАЧ
1.1 (Вариант 4) Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 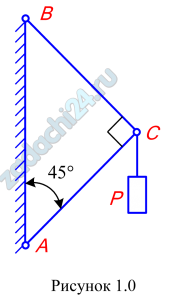
Таблица 1
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
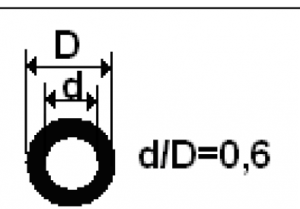 | 10 | 160 | 100 |
Ответ: NBC=7,1 кН, NAC=-7,1 кН, D=15,0 мм, d=9,0 мм.
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.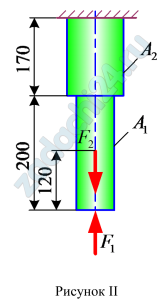
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 | F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
Ответ: Δl=0,113·10-3 м.
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.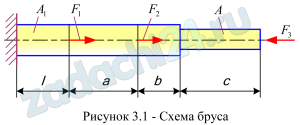
Таблица 3.1 — Исходные данные
| A1/A | b/l | F1/F | c/l | F2/F | Материал | № схемы | a/l | F3/F |
| 1,70 | 2,0 | -2 | 1,0 | -4 | Магн. спл. МА — 5 | 1 | 2,0 | 2,0 |
Таблица 3.2 — Механические характеристики материала
| 1 Пластичные материалы | ||||||
| Материал | Марка | σт, МПа | σв, МПа | τт, МПа | Е·10-5 МПа. | μ |
| Магниевый сплав | МА-5 | 220 | 300 | 160 | 0,72 | 0,27 |
Дано: схема бруса (рис.3.1) А1=1,7А; b=2l; F1=-2F; c=l; F2=-4F; Материал — Магниевый сплав МА-5; a=2l; F3=2F; А=200 мм²; l=200 мм; s=2.
Из табл.3.2 находим σт=220 МПа; Е=0,72·105 МПа.
Ответ: F=4672 H, Δamax=1,05 мм, Δlamax=0,46 мм.
1.4 (Вариант 1177) Для консольного бруса переменного сечения (рис.1.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также наибольшее удлинение участка a.![Для консольного бруса переменного сечения (рис.1.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также наибольшее удлинение участка a. Принять:А=200 мм², l=200 мм, s=[k]=2, остальные данные взять из табл.1.1 и табл. 1.9.](https://zadachi24.ru/wp-content/uploads/2016/12/sopromat_1.4.0-300x151.png)
Принять:А=200 мм², l=200 мм, s=[k]=2, остальные данные взять из табл.1.1 и табл. 1.9.
Таблица 1.1
| A1/A | b/l | F1/F | c/l | F2/F | Материал | № схемы | a/l | F3/F |
| 1,20 | 1,5 | -1 | 2,0 | -3 | Алюмин. сплав АК-4 | II | 2,5 | 1,0 |
Ответ: F=15500 H, Δamax=1,040 мм, Δlamax=-0,448 мм.
1.5 (Вариант 39) Расчеты на прочность и жесткость при растяжении (сжатии)
Ступенчатый стержень находится под действием продольных сил F, приложенных по концам или в центре соответствующего участка стержня. Материал стержня – сталь с допускаемым напряжением [σ]=200 МПа, модуль продольной упругости Е=2·105 МПа.
Требуется:
1 Построить эпюры: продольных усилий, напряжений, перемещений;
2 Проверить прочность стержня.![Тышкевич, В. Н. Сопротивление материалов Задание 3 Расчеты на прочность и жесткость при растяжении (сжатии) Ступенчатый стержень находится под действием продольных сил F, приложенных по концам или в центре соответствующего участка стержня. Материал стержня – сталь с допускаемым напряжением [σ]=200 МПа, модуль продольной упругости Е=2·105 МПа. Требуется: 1 Построить эпюры: продольных усилий, напряжений, перемещений; 2 Проверить прочность стержня.](https://zadachi24.ru/wp-content/uploads/2017/01/sopromat-1.5.0-260x300.png)
Таблица 3.1 – Исходные данные
| Длина участка, см | Площадь поперечного сечения, см2 | ||||
| l1 | l2 | l3 | A1 | A2 | A3 |
| 60 | 30 | 48 | 10 | 4 | 8 |
Продолжение таблицы 3.1
| Нагрузка, кН | |||||
| F1 | F2 | F3 | F4 | F5 | F6 |
| 140 | 80 | — | 100 | — | — |
Ответ: условие прочности не выполняется, перенапряжение составляет 25%.
1.6 Построение эпюр при растяжении (сжатии)
Стальной двухступенчатый брус, длины ступеней которого указаны на рисунке 1, нагружен силами F1, F2, F3 (положение точек приложения сил задано размерами). Построить эпюры продольных сил и нормальных напряжений по длине бруса, а также эпюру перемещений поперечных сечений бруса. Определить перемещение Δl свободного конца бруса, приняв Е=2·105 МПа. Числовые значения сил F1, F2, F3, а также площади поперечных сечений ступеней A1 и A2 для своего варианта взять из таблицы 1.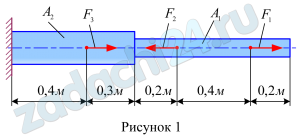
Таблица 1
| Вариант | F1 | F2 | F3 | A1 | A2 |
| кН | см2 | ||||
| 3 | 24 | 11 | 27 | 1,5 | 4,0 |
Ответ: Δl=656 мкм.
1.7 (Вариант 165456) Стальной стержень (Е=2·105 МПа) находится под действием продольной силы Р. Постройте эпюры продольных сил N, напряжений σ, перемещений Δ. Проверьте прочность стержня. Данные взять из табл. П.2.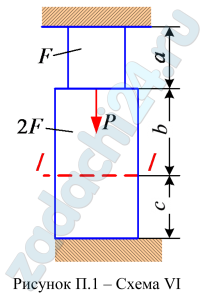
Таблица П.2
| Схема по рис. П1, П2, П3, П4 | F, см2 | a | b | c | Р·102, Н |
| м | |||||
| VI | 15 | 2,4 | 2,5 | 1,6 | 1400 |
Варианты задачи: 131519, 186891.
1.8 Растяжение-сжатие прямого бруса
Дан брус, нагруженный, как показано на рисунке 1. Цифровые данные – в таблице 2.
Требуется:
1. Определить реакцию в заделке (если требуется).
2. Составить выражения для продольных сил на каждом участке бруса.
3. Определить значений продольных сил на границе каждого участка.
4. Рассчитать нормальные напряжения на границе каждого участка.
5. Вычислить абсолютную деформацию каждого участка, а также перемещения всех граничных сечений. При необходимости определить экстремальные значения перемещений.
6. Построить эпюры
— продольных сил;
— нормальных напряжений;
— перемещений.
Таблица 2
| №№ п.п. | l, м | P1, кН | q1, кН/м | А1, мм2 | Е·10-5, МПа |
| 9 | 0,72 | 41 | 55 | 82 | 1,4 |
Принять: P2=1,25P1; P3=1,4P1; A2=0,85A1; A3=0,75A1; q2=1,1q1.
1.9 (Вариант 531) Тема «Растяжение – сжатие»
Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется:
1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине;
2) определить размеры поперечного сечения (сторону квадрата или диаметр);
3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине;
4) вычислить деформации участков стержня и построить эпюру перемещений δ.
Исходные цифровые данные приведены в табл. 1. ![Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 4 Тема «Растяжение – сжатие» Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется: 1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине; 2) определить размеры поперечного сечения (сторону квадрата или диаметр); 3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине; 4) вычислить деформации участков стержня и построить эпюру перемещений δ. Исходные цифровые данные приведены в табл. 1.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_1.9.0-300x157.png)
Таблица 1
| l1, м | l2, м | l3, м | l4, м |
| 0,9 | 0,8 | 1,5 | 0,9 |
Продолжение таблицы 1
| F1, МН | F2, МН | F3, МН | Номер схемы (рис. 1) | Форма сечения |
| 1,4 | 0,4 | 1,7 | 1 | Квадрат |
Методические указания
1.10 (Вариант 6) Практическая работа на растяжение и сжатие
Цель: Научиться строить эпюры продольных сил Nz и нормальных напряжений σ и производить проверочный расчет.
Задача. Двухступенчатый брус в соответствии с рисунком нагружен силами Р1=15 кН; Р2=10 кН; Р3=5 кН и площадями поперечных сечений А1=1,2 см²; А2=2,0 см².
а) построить эпюры продольных сил Nz и нормальных напряжений σ;
б) проверить условие прочности, если [σ]=160 МПа;
в) определить удлинение (укорочение) бруса Δl, если а=0,2 м, b=0,4 м, с=0,5 м, Е=2·105 МПа.![Практическая работа на растяжение и сжатие Цель: Научиться строить эпюры продольных сил Nz и нормальных напряжений σ и производить проверочный расчет. Задача. Двухступенчатый брус в соответствии с рисунком нагружен силами Р1=15 кН; Р2=10 кН; Р3=5 кН и площадями поперечных сечений А1=1,2 см²; А2=2,0 см². а) построить эпюры продольных сил Nz и нормальных напряжений σ; б) проверить условие прочности, если [σ]=160 МПа; в) определить удлинение (укорочение) бруса Δl, если а=0,2 м, b=0,4 м, с=0,5 м, Е=2·105 МПа.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_1.10.0-300x129.png)
Ответ: условие прочности выполняется.
Источник
Задачи на растяжение и сжатие (задачи по сопромату)
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
