Равномерно распределенная нагрузка на растяжение
Содержание статьи
—
1.
d F. , .
.
.
,
.
, .
, .
2.
, .
.
1. . z:
, ,
RE = 2qa.
2. Nz, , W.
Nz.
.
,
,
.
. . , Nz, . :
.
W.
.
. :
Wo = WE = 0,
W.
3.
, , , F1= 100 , F2= 50 , q= 40 /, = 1 , b = 2 , = 1,5 , = 2×105 , S= 0,2 2.
.
1. , , CD
2.
CD
CB
z2=1,5 , N2=-100 ,
z2=3,5 , N2=-20 ,
B
1)
2)
4.
(. ). 2 . : =40 , =60 , =50 ; =20 /.
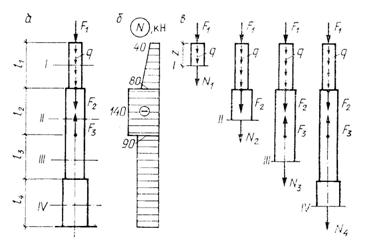
:
. () () (. ).
(),
=0 ;
=2 ,
:
,
,
,
, , () . (. ), . , , , , , .
5.
(. ).
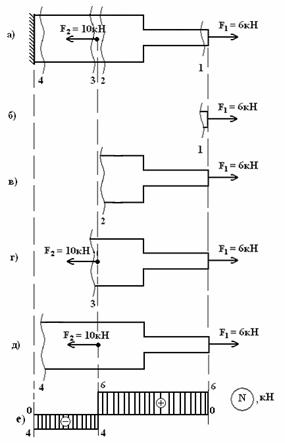
.
1. . , , -, N.
2. , .
3. . . , .
4. N. 1 (. ) N1 = F1 = 6; 2 (. ) N2 = F1 = 6. : N1, N2> 0, F1 . N1, N2, , ( ) . + (. ). . 3 (. ) N3 = F1 F2 = 6 10 = — 4; 4 (. ) N4 = F1 F2 = 6 10 = — 4 . N3, N4< 0. -. N1 N4 (. ).
5. .
6. . , . (1) F1 = 6 6; F2 =10 6 + 4 =10; , 4 (4) , . .
6.
.
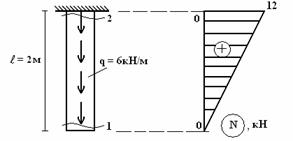
.
1. -, N.
2. , .
3. .
4. . , . . . N1 = 0; .
5. N1, N2 , , (. .).
6. , .
7. : — , . , ( ).
7.
.
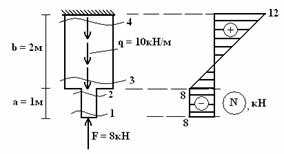
.
1. -.
2. .
3. .
4. : N1 = -F= -8 ; N2 = -F = -8 . , , , . ; . N3< 0, ; N4> 0 .
5. , (. .).
6. : , ; . (1) F = 8 , 8.
8.
Nz , .
.
, . Nz . (. ) (. ). DE , , .. NED = +F. D NDE = NED = F ND = ND 3F = 2F( dz, CD DE).
, 3F Nz, 3F . CD ND = ND= 2F. C ND = 2F N = ND+ 5F = 3F. 5F. C N = N=3F. , Nz : N= 3F N= N 2F = F. ( ), 2F . Nz .
9.
, , , , . .
.
z :
, , q = 3F/a.
Nz . CD , (q = 0). (q = const). D, , Nz , . . 2F , NAB = -2F. NB = NA = -2F . CD ND = 4F.
10.
, (), . (). .
.
1, 2, 3, 4 , . , ; . . . 1 F1 = 20 , . 12 , , .. q12 =(60-20)/2 = 20 /. . 2 F2 = 100 . 23 , . 3 F3 = 80 ( ). 34 q34 = (-40 — 40)/1 = -80 /, . , 4 F4 = 40 , .
11.
A1/A2=2 , . . , . ( .)
.
N . :
.
, , :
;
;
.
N . x.
,
.
, .
N. . N : , ; F1 = 10 , F2 = 40 , q1 = 15 /, q2 = 20 /.
, (. ). , (.. ) , .
. , . , . , , . , , , . , , , :
, ,
;
, .
A1, , . 2 : .
. ( ) , .
12.
, . .
.
. , . . , .
I I. , N1 (. ). , :
N1 = F.
, () N1 . N1= F I I (. ).
II II , , N2 (. ). :
N2 = F.
III III (. ):
N3 = F
IV IV (. ):
N4= 0.
N2, N3, N4 , (. ). , . . , , .
:
(. ) , ( III).
13.
I I , , = 20 = 2 , = 10 = 1 , = 10 = 1 , = 60º (. .).
) )
.
:
) ;
) , , (, );
) N, , .. , ;
) N:
; ;
= 1 = 10 ,
.. .
, , .
14.
, = 40 = 4 , = 30 = 3 , = 80 = 8 ; = 160 = 1600 /2 (. .).
.
1. , 3- (. ):
1 1 = 4000 = 40 ,
2 2 = 4000 + 3000 = 1000 = 10 ,
3 3 = 4000 + 3000 + 8000=7000 = 70 .
2. , , , , , , .. N (. ).
3. , ( ), ..
,
.
N3>N2>N1. 3, = 7000 = 70 .
; .
15.
(), F1 = 150 = 15 , F2 = 100 = 10 , = 30 c, b = 20 , = 15 A = 10 2 :
1. .
2. .
3. I I (. .).
) ) )
.
1. . ( + b) c. ,
= = 15103 = 150 ();
:
= = 15 20= 5 = 50 ().
(. ).
2. .
b 2=20 2.
:
(. ).
2. :
= 0,00973 0,00375 = 0,00562 = 0,0562 .
3. , I I b c, ..
16.
() 1 2 (. ).
:
1. N, σ ;
2. : 1=2 ; 2=3,2 , =160 .
.
N . .
.
.
.
.
. .
.
. .
17.
( /2) ; , 2, 2 (. .). . , ( ) /2, . .
.
1. , .
, , . :
.
2. .
(. ). , () .
(). .
1 1. ( ) (. ). 1 1 . , . . , . , 1 1 . ,
.
2 2 (. ). , (, 2 2 ). , , . , 2 2 , , . :
.
3 3 (. ). , . () R. :
.
, , , . . :
.
: , , , , , .
, , , . , , .
, , . , .
, z(. ). . , .
, ( ) .
.
, , , . , . , .
3. .
, k (),
,
k .
/2,
/2,
/2.
(. ). , . , N, , , .
4. .
( ) , , . , , , . , , . : .
/2.
.
/2 > /2,
, .
, , 2, .
, .
:
2.
2.
5. .
,
E , .
.
, 1,7 .
18.
(. .1) (), , F= 30 , l= 0,4 = 160 :
1. .
2. .
3. .
4. -.
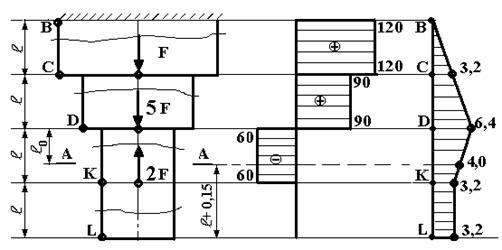
N, ,
) ) )
.1
.
1. . N.
KL: , . , N1, , .. ( 2). , Z, N1:
; N1 = 0;
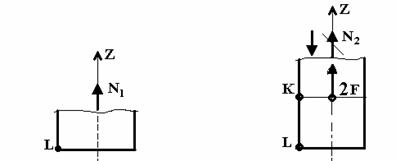
. 2 . 3
DK: KL DK; , N2 , ( 3) :
; 2F + N2= 0;
N2 = — 2F = -2×30 = — 60 .
N2 , , .. , . , N2 , .
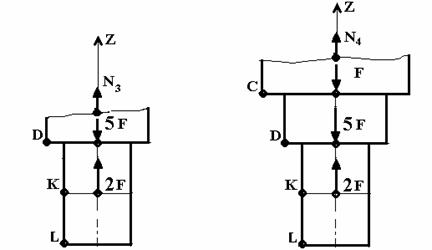
. 4 .5
D: N3 KL DK ( 4).
; 2F 5F+ N3= 0;
N3 = 5F 2F = 3F = 3 ×30 = 90 .
N3. , N3 .
C: (. 5) :
; 2F 5F — F+ N4= 0;
N4 = 5F + F 2F = 4F = 4×30 = 120 .
N4 .
. , () ( 4,):
1. KL: N1 = 0;
2. DK: N2 = 60 . , .
3. D: N3 = 90 , , , .
4. : N4 = 120 .
: , .
2. . .
; .
KL DK: KL DK, ,
D:
:
3. .
:
.
.
() l :
.
KL: .. N1 = 0;
DK:
CD:
C:
:
(0 0,32 + 0,32 + 0,32 + 0,32)×10-3 = 0,32×10-3.
( ), .. , .. .
: .
:
;
;
.
(.1, ) ; .
4. . — D l0 (. 1,):
;
.
1 — . , (. .1,).
19.
. .
) ) ) |
.
1.
, Z,
,
.
2. N N(z)
, , . . , ( 1, ).
.
.
, — (. ).
, . ,
.
3.
.
.
. , .
,
. , .
, .
,
.
,
.
, .
, 5,8 %.
.
,
.
4.
,
,
; i- ; i- ; i- , i- .
.
, − .
, . . .
.
.
− .
.
.
.
, — ( 1, ).
5.
(5), :
.
:
.
, .
20.
, , P q. .
) ) ) |
.
1.
(. )
,
.
2.
. ( 1, )
.
, — .
. , .
. (. ).
.
, .
. . . :
; .
. .
.
:
1) ;
2) , .. − , ,
, , .
.
3.
.
− . .
(), , . h b. :
,
.
, . :
,
.
, .. . .
4.
:
,
.
. , , :
.
, .. . , .
.
.
− . ,
.
(. ). .
—
21.
d, CD , F, . , [] .
F :
—
,
—
.
o .
CD
.
mnrs,
.
, .
22.
A1/A2 =2 (. ). . .
.
. , . , , . .
,
,
.
, . , q , , N , , A1 , A2 (. ). g, (. ).
() . . . F , l; G . . , .. . , l1, , . F F1, F2 . l1: . ,
.
, F2, , , .
.
.
, , . , . , () ( . ) , :
.
, . .
23.
, . . a= 0,4 ; III IV = 20 2; F= 0,5 , = 0,0078 /3 = 76,44 /3.
.
. I I (. ) , N1 (. ). I I I, , x (. ), . , , , :
, 2, x. :
.
, . N1 (x = 0): N1(x= 0) = 500 (x = a= 0,5 ): N1 ( = 0,5 ) =
(. ). , , .
II II , I I. II II . (. )
, II II.
N2 (= 0,5 ):
( = max = 1 ):
N2 (. ).
III III (. )
; .
N3 N3(=0) = 194,2 ; N3 ( = a = 0,5 ) = 117,8 . N3 .
, , IV IV (. )
I I II II, .
.. N4 ( = 0,5 ) = 382,2 , N4 ( = 1 ) = 458,64 . N4 (. ).
, , .
:
, , (. ), .. .
24.
: (. .) 2l, A, F, q .
: N.
N
.
1.
Z:
2.
F, , q , , :
— , , N F ;
— , , N F, ,q.
3.
, , . N1N2 , , .
4. N
N :
— ;
— .
— ;
— .
— ;
.
N (. .).
. — . N :
.
—
25.
, . . . a = 0,5 ; = 10 2; F = 10 .
.
. . (1.7). . . , :
, , .. .
26.
, . . = 76440 /3.
.
. .
. (. ) , . . .
+ , , .. (. ).
(. ). . (. ) ,
, .
27.
, (. . ):
1. ;
2. Nz , ;
3. Nz ;
4. .
: = 20 ; l1 = l2 = l3 = 0,4 ; = /2; F1 = 2; F2 = 2; F3 = 2; = 78 /3 .
.
1. . Nz , , , , Fi g, , .
, =const, :
1 — 0 ( );
2 — ;
3 — D.
, .
2. Nz, sz , . .
1 (0 — ) .
1 — 1 z1 ( 0), . , , (. ). z , :
.
, :
.
:
,
:
/2.
, z1 , () , ..
z1 = 0
z1 = 0,4 ;
/2.
, , . . , .
2 ( — ) .
2-2 z2 (. ). .
: ; ; = 20 , .
:
,
= = .
, :
/2.
:
z2 = 0,4 ,
/2;
z2 = 0,8 ,
/2.
3 ( — D) .
(. ) , :
,
.
:
/2.
:
z3 = 0,8 (0,8) = -19,5 (0,8 + 0,43364) = -24,056 ,
(0,8) = -78 (0,8 + 0,43364) = -96,224 /2;
z3 = 1,2 (1,2) = -19,5 (1,2 + 0,43364) = -31,856 ,
/2.
3. Nz . z Nz (. . , ). :
— Nz ;
— .
(. , ) , .
4. .
.
:
, , Nz Ei Fi . ,
.
28.
, .
.
(). dx:
dG dx:
,
, .
, = 0 () = 0, .. .
, ()
,
.. .
— » -«
: KarimovI@rambler.ru
: , 450071, ., 21
Источник
Распределенная нагрузка на балку — формулы, условия и примеры расчета
Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве — по её площади.
Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м3] для объемной конструкции, в [H/м2] — для площади, для линейной — в [H/м].
Продемонстрируем это на рисунке:
Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:
Q = q ∗ AB⌈H⌉
здесь AB является тяжестью, q — интенсивностью, которая измеряется в [H/м].
Примечательно, что сила приложена к середине данного отрезка AB.
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:
Q = qmax ∗ AB/2
где qmax — максимальная интенсивность [Н/м].
Q приложена к точке C, где AC равно: AC = 2/3 AB
Рассматривая функцию q(x), представленную на рисунке:
можно высчитать значение эквивалентной силы по формуле:
Равномерно и неравномерно распределенная нагрузка на балку
Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а.
Единицы измерения распределённой нагрузки [Н/м].
Её также можно заменить на величину Q, которая приложена в середину AB.
Составим формулу: Q = q∗a
Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.
При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.
Пример решения задач с распределенной нагрузкой
Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.
Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы — R, ось симметрии Оx, а 2α — это центральный угол. Представим это на рисунке:
Выделим элемент сектора трубы ∆ϕ.
Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:
Проекция результирующей тяги на ось Оx является:
Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:
AB является хордой, которая стягивает дугу.
В нашей задаче сосуд — это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м2].
Разделим цилиндр вдоль его диаметра.
Исходя из этого, равнодействующая результирующих сил определяется по формуле:
где d — это внутренний диаметр цилиндра, h — его высота.
Формулу также можно записать следующим образом:
Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:
Изобразим баллон в момент разрыва:
Учтём a — толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:
Важную роль при решении практических задач также играет эпюра распределенной нагрузки — плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью — силой, которая распространяется на единицы площади, объема или длины.
Источник
Растяжение-сжатие.
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии — отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность — свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость — свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость — свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость — свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой — на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
