Сопромат как построить эпюры растяжение

Построение эпюр продольных сил — формулы, условия и примеры решения задач

Построение эпюр продольных сил — это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.

Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.

Но всему свое время. Сначала немного о терминах.

Основные понятия

Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.

Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок — часть балки с неизменным сечением и характерной нагрузкой.

Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие — отрицательными.

В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).

Что такое эпюра продольных сил

Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра — наглядное графическое изображение изменения нагрузки по всей длине конструкции.

Как построить эпюру продольных сил

Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.

Сопротивление рассчитывается по формуле:

где:

• Fl — действующие на участке l силы (Н);

• ql — распределенные нагрузки (Н/м).

Порядок построения:

1. Рисуется схема балки и механизмов закрепления;

2. Производится разделение на участки;

3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:

Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;

4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные — ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

Рис. 1. Эпюра продольных сил

Рассмотрим случай:

F1 = 5 (кН);

F2 = 3 (кН);

F3 = 6 (кН).

Вычислим:

Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.

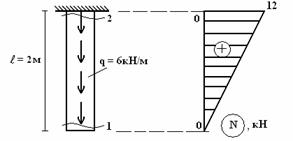
Пример построения эпюр и решения задач

Построить эпюру сил для следующего случая (рис. 2):

Рис. 2

Дано:

Решение.

Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:

Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.

Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.

По полученным данным строим эпюру (рис. 3).

Рис. 3

Заключение

Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.

В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.

Источник

—

1.

d F. , .

.

.

,

.

, .

, .

2.

, .

.

1. . z:

, ,

RE = 2qa.

2. Nz, , W.

Nz.

.

,

,

.

. . , Nz, . :

.

W.

.

. :

Wo = WE = 0,

W.

3.

, , , F1= 100 , F2= 50 , q= 40 /, = 1 , b = 2 , = 1,5 , = 2×105 , S= 0,2 2.

.

1. , , CD

2.

CD

CB

z2=1,5 , N2=-100 ,

z2=3,5 , N2=-20 ,

B

1)

2)

4.

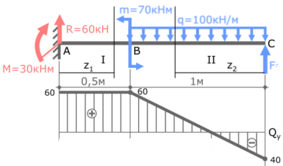
(. ). 2 . : =40 , =60 , =50 ; =20 /.

:

. () () (. ).

(),

=0 ;

=2 ,

:

,

,

,

, , () . (. ), . , , , , , .

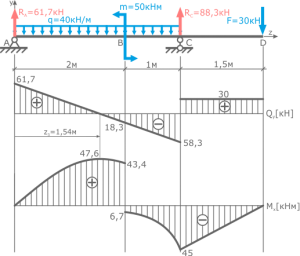
5.

(. ).

.

1. . , , -, N.

2. , .

3. . . , .

4. N. 1 (. ) N1 = F1 = 6; 2 (. ) N2 = F1 = 6. : N1, N2> 0, F1 . N1, N2, , ( ) . + (. ). . 3 (. ) N3 = F1 F2 = 6 10 = — 4; 4 (. ) N4 = F1 F2 = 6 10 = — 4 . N3, N4< 0. -. N1 N4 (. ).

5. .

6. . , . (1) F1 = 6 6; F2 =10 6 + 4 =10; , 4 (4) , . .

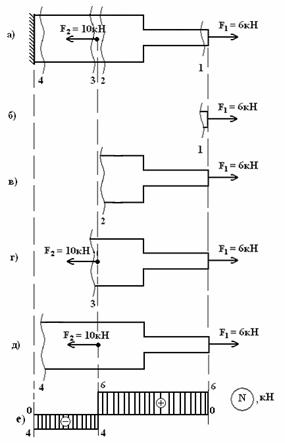
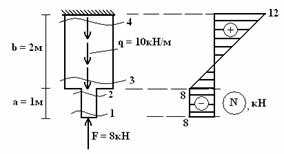
6.

.

.

1. -, N.

2. , .

3. .

4. . , . . . N1 = 0; .

5. N1, N2 , , (. .).

6. , .

7. : — , . , ( ).

7.

.

.

1. -.

2. .

3. .

4. : N1 = -F= -8 ; N2 = -F = -8 . , , , . ; . N3< 0, ; N4> 0 .

5. , (. .).

6. : , ; . (1) F = 8 , 8.

8.

Nz , .

.

, . Nz . (. ) (. ). DE , , .. NED = +F. D NDE = NED = F ND = ND 3F = 2F( dz, CD DE).

, 3F Nz, 3F . CD ND = ND= 2F. C ND = 2F N = ND+ 5F = 3F. 5F. C N = N=3F. , Nz : N= 3F N= N 2F = F. ( ), 2F . Nz .

9.

, , , , . .

.

z :

, , q = 3F/a.

Nz . CD , (q = 0). (q = const). D, , Nz , . . 2F , NAB = -2F. NB = NA = -2F . CD ND = 4F.

10.

, (), . (). .

.

1, 2, 3, 4 , . , ; . . . 1 F1 = 20 , . 12 , , .. q12 =(60-20)/2 = 20 /. . 2 F2 = 100 . 23 , . 3 F3 = 80 ( ). 34 q34 = (-40 — 40)/1 = -80 /, . , 4 F4 = 40 , .

11.

A1/A2=2 , . . , . ( .)

.

N . :

.

, , :

;

;

.

N . x.

,

.

, .

N. . N : , ; F1 = 10 , F2 = 40 , q1 = 15 /, q2 = 20 /.

, (. ). , (.. ) , .

. , . , . , , . , , , . , , , :

, ,

;

, .

A1, , . 2 : .

. ( ) , .

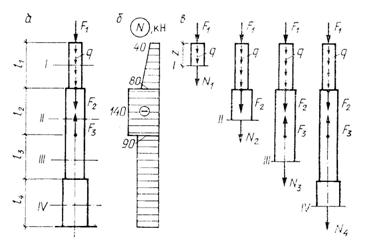
12.

, . .

.

. , . . , .

I I. , N1 (. ). , :

N1 = F.

, () N1 . N1= F I I (. ).

II II , , N2 (. ). :

N2 = F.

III III (. ):

N3 = F

IV IV (. ):

N4= 0.

N2, N3, N4 , (. ). , . . , , .

:

(. ) , ( III).

13.

I I , , = 20 = 2 , = 10 = 1 , = 10 = 1 , = 60º (. .).

) )

.

:

) ;

) , , (, );

) N, , .. , ;

) N:

; ;

= 1 = 10 ,

.. .

, , .

14.

, = 40 = 4 , = 30 = 3 , = 80 = 8 ; = 160 = 1600 /2 (. .).

.

1. , 3- (. ):

1 1 = 4000 = 40 ,

2 2 = 4000 + 3000 = 1000 = 10 ,

3 3 = 4000 + 3000 + 8000=7000 = 70 .

2. , , , , , , .. N (. ).

3. , ( ), ..

,

.

N3>N2>N1. 3, = 7000 = 70 .

; .

15.

(), F1 = 150 = 15 , F2 = 100 = 10 , = 30 c, b = 20 , = 15 A = 10 2 :

1. .

2. .

3. I I (. .).

) ) )

.

1. . ( + b) c. ,

= = 15103 = 150 ();

:

= = 15 20= 5 = 50 ().

(. ).

2. .

b 2=20 2.

:

(. ).

2. :

= 0,00973 0,00375 = 0,00562 = 0,0562 .

3. , I I b c, ..

16.

() 1 2 (. ).

:

1. N, σ ;

2. : 1=2 ; 2=3,2 , =160 .

.

N . .

.

.

.

.

. .

.

. .

17.

( /2) ; , 2, 2 (. .). . , ( ) /2, . .

.

1. , .

, , . :

.

2. .

(. ). , () .

(). .

1 1. ( ) (. ). 1 1 . , . . , . , 1 1 . ,

.

2 2 (. ). , (, 2 2 ). , , . , 2 2 , , . :

.

3 3 (. ). , . () R. :

.

, , , . . :

.

: , , , , , .

, , , . , , .

, , . , .

, z(. ). . , .

, ( ) .

.

, , , . , . , .

3. .

, k (),

,

k .

/2,

/2,

/2.

(. ). , . , N, , , .

4. .

( ) , , . , , , . , , . : .

/2.

.

/2 > /2,

, .

, , 2, .

, .

:

2.

2.

5. .

,

E , .

.

, 1,7 .

18.

(. .1) (), , F= 30 , l= 0,4 = 160 :

1. .

2. .

3. .

4. -.

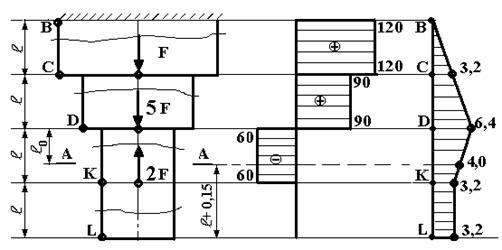
N, ,

) ) )

.1

.

1. . N.

KL: , . , N1, , .. ( 2). , Z, N1:

; N1 = 0;

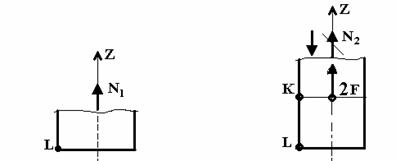
. 2 . 3

DK: KL DK; , N2 , ( 3) :

; 2F + N2= 0;

N2 = — 2F = -2×30 = — 60 .

N2 , , .. , . , N2 , .

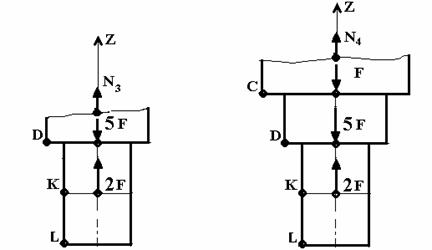
. 4 .5

D: N3 KL DK ( 4).

; 2F 5F+ N3= 0;

N3 = 5F 2F = 3F = 3 ×30 = 90 .

N3. , N3 .

C: (. 5) :

; 2F 5F — F+ N4= 0;

N4 = 5F + F 2F = 4F = 4×30 = 120 .

N4 .

. , () ( 4,):

1. KL: N1 = 0;

2. DK: N2 = 60 . , .

3. D: N3 = 90 , , , .

4. : N4 = 120 .

: , .

2. . .

; .

KL DK: KL DK, ,

D:

:

3. .

:

.

.

() l :

.

KL: .. N1 = 0;

DK:

CD:

C:

:

(0 0,32 + 0,32 + 0,32 + 0,32)×10-3 = 0,32×10-3.

( ), .. , .. .

: .

:

;

;

.

(.1, ) ; .

4. . — D l0 (. 1,):

;

.

1 — . , (. .1,).

19.

. .

.

1.

, Z,

,

.

2. N N(z)

, , . . , ( 1, ).

.

.

, — (. ).

, . ,

.

3.

.

.

. , .

,

. , .

, .

,

.

,

.

, .

, 5,8 %.

.

,

.

4.

,

,

; i- ; i- ; i- , i- .

.

, − .

, . . .

.

.

− .

.

.

.

, — ( 1, ).

5.

(5), :

.

:

.

, .

20.

, , P q. .

.

1.

(. )

,

.

2.

. ( 1, )

.

, — .

. , .

. (. ).

.

, .

. . . :

; .

. .

.

:

1) ;

2) , .. − , ,

, , .

.

3.

.

− . .

(), , . h b. :

,

.

, . :

,

.

, .. . .

4.

:

,

.

. , , :

.

, .. . , .

.

.

− . ,

.

(. ). .

—

21.

d, CD , F, . , [] .

F :

—

,

—

.

o .

CD

.

mnrs,

.

, .

22.

A1/A2 =2 (. ). . .

.

. , . , , . .

,

,

.

, . , q , , N , , A1 , A2 (. ). g, (. ).

() . . . F , l; G . . , .. . , l1, , . F F1, F2 . l1: . ,

.

, F2, , , .

.

.

, , . , . , () ( . ) , :

.

, . .

23.

, . . a= 0,4 ; III IV = 20 2; F= 0,5 , = 0,0078 /3 = 76,44 /3.

.

. I I (. ) , N1 (. ). I I I, , x (. ), . , , , :

, 2, x. :

.

, . N1 (x = 0): N1(x= 0) = 500 (x = a= 0,5 ): N1 ( = 0,5 ) =

(. ). , , .

II II , I I. II II . (. )

, II II.

N2 (= 0,5 ):

( = max = 1 ):

N2 (. ).

III III (. )

; .

N3 N3(=0) = 194,2 ; N3 ( = a = 0,5 ) = 117,8 . N3 .

, , IV IV (. )

I I II II, .

.. N4 ( = 0,5 ) = 382,2 , N4 ( = 1 ) = 458,64 . N4 (. ).

, , .

:

, , (. ), .. .

24.

: (. .) 2l, A, F, q .

: N.

N

.

1.

Z:

2.

F, , q , , :

— , , N F ;

— , , N F, ,q.

3.

, , . N1N2 , , .

4. N

N :

— ;

— .

— ;

— .

— ;

.

N (. .).

. — . N :

.

—

25.

, . . . a = 0,5 ; = 10 2; F = 10 .

.

. . (1.7). . . , :

, , .. .

26.

, . . = 76440 /3.

.

. .

. (. ) , . . .

+ , , .. (. ).

(. ). . (. ) ,

, .

27.

, (. . ):

1. ;

2. Nz , ;

3. Nz ;

4. .

: = 20 ; l1 = l2 = l3 = 0,4 ; = /2; F1 = 2; F2 = 2; F3 = 2; = 78 /3 .

.

1. . Nz , , , , Fi g, , .

, =const, :

1 — 0 ( );

2 — ;

3 — D.

, .

2. Nz, sz , . .

1 (0 — ) .

1 — 1 z1 ( 0), . , , (. ). z , :

.

, :

.

:

,

:

/2.

, z1 , () , ..

z1 = 0

z1 = 0,4 ;

/2.

, , . . , .

2 ( — ) .

2-2 z2 (. ). .

: ; ; = 20 , .

:

,

= = .

, :

/2.

:

z2 = 0,4 ,

/2;

z2 = 0,8 ,

/2.

3 ( — D) .

(. ) , :

,

.

:

/2.

:

z3 = 0,8 (0,8) = -19,5 (0,8 + 0,43364) = -24,056 ,

(0,8) = -78 (0,8 + 0,43364) = -96,224 /2;

z3 = 1,2 (1,2) = -19,5 (1,2 + 0,43364) = -31,856 ,

/2.

3. Nz . z Nz (. . , ). :

— Nz ;

— .

(. , ) , .

4. .

.

:

, , Nz Ei Fi . ,

.

28.

, .

.

(). dx:

dG dx:

,

, .

, = 0 () = 0, .. .

, ()

,

.. .

— » -«

: KarimovI@rambler.ru

: , 450071, ., 21

Источник