Задачи на растяжение и подбор сечений
Содержание статьи
Решение типовых задач по сопромату.
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
1 Растяжение и сжатие
1.1 (Вариант 4) Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 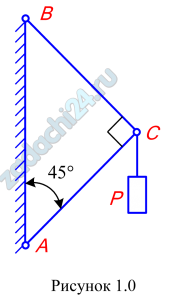
Таблица 1
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
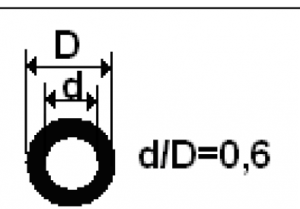 | 10 | 160 | 100 |
Ответ: NBC=7,1 кН, NAC=-7,1 кН, D=15,0 мм, d=9,0 мм.
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.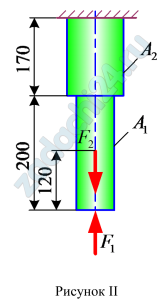
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 | F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
Ответ: Δl=0,113·10-3 м.
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.
Источник
Тема: Решение задач по теме «Растяжение , сжатие»
Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ!
Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
Время выполнения работы – 1 час
Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.
Величина последней равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть стержня
N=∑ FKZ (1)
Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т.е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.
Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение, которое определяется по формуле:
σ =N/А
где А- площадь поперечного сечения стержня.
При решении первой задачи от студента требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.
Последовательность построения эпюр продольных сил:
Разбиваем стержень на участки, ограниченные точками приложения сил ( нумерацию участков ведём от незакрепленного конца ).
Используя метод сечений, определяем величину продольных сил в сечении каждого участка.
Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх ( или в право ) отрицательное — вниз ( или влево).
Последовательность построения эпюр нормальных напряжений.
Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения
Строим эпюру нормальных сил
по формуле 1 определяем нормальные напряжения на каждом участке
По полученным значениям в масштабе строим эпюру нормальных напряжений.
Удлинение ( укорочение ) стержня определяется по формуле Гука .
где Е – модуль Юнга ( для стали Е=2·10 5 МПа ).
Удлинение (укорочение) определяется на каждом участке стержня, а затем находят алгебраическую сумму полученных значений. Это будет ∆lстержня. Если ∆l положительна, то брус удлиняется, если ∆l отрицательна, то укорачивается.
При решении ряда задач необходимо ясно представлять смысл условия прочности при растяжении – сжатии, знать, что исходя из условия прочности, можно производить три вида расчётов:
а) проверочный, при котором проверяется выполнено ли условие прочности σ≤ [σ] ( или n≥ [n]);
б) определение допускаемой нагрузки;
в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность.
Студенты должны также уметь пользоваться в ходе решения всеми необходимыми формулами, расчётными зависимостями и правильно выполнять вычисления.
II. Вопросы для самопроверки
2.1. Как нужно нагрузить прямой брус, чтобы он работал на растяжение — сжатие?
2.2 Как определяется напряжение в любой точке поперечного сечения при растяжении (сжатии)?
2.3. Каков физический смысл модуля продольной упругости Е?
2.4. Что такое допускаемое напряжение и как оно выбирается в зависимости от механических свойств материала?
2.5. Сколько различных видов расчёта, и какие расчеты можно проводить, используя условие прочности?
адача. Проверить прочность стального стержня при заданых допускаемых напряжениях 160МПа. (решение задач по технической механике)
А лгоритм решения
- Находим неизвестные внешние усилия (силы, моменты, реакции опор)
- Разбиваем на расчетные участки (границы расчетных участков определяются изменением нагрузки, площади сечения, материала).
- Пользуясь методом сечений определяем продольные силы. (Метод сечений: Разрезаем стержень, Отбрасываем одну из частей, Заменяем действие отброшенной части внутренними силами, составляем Уравнения равновесия рассматриваемой части)
- Строим эпюру продольных сил
- определяем нормальные напряжения на участках
- Строим эпюру перемещений
- Проверяем прочность стержня (в случае, если материал стержня по разному работает на растяжениеи сжатие, проверяем прочность отдельно на растяжения и сжатие)
- Определяем перемещения на каждом участке (перемещение в конце участка равняется сумме перемещений в начале участка и перемещению на данном участке)
9. Строим эпюру перемещений
При решении задачи пренебрегаем собственным весом стержя.
При жестко закрепленном стержне вначале можно не определять реакции в опоре, а строить эпюры, идя со свободного конца стержня. При этом реакцию в опоре можно определить по эпюре продольных сил
Порядок решения типовых задач
Задача №1
Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆l свободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2?;А 2 =2см2?
Первая задача требует от студента умения строить эпюры продольных сил, нормальных напряжений и определять удлинения и укорочения бруса.
Последовательность решения задачи
Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.
Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
Перемещение свободного конча бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
Решение:
Разбиваем брус на участки.
Определяем ординаты эпюры N на участках бруса:
N1= — F1= -30кН
N2= — F2= -30кН
N3= -F1+F2= -30+40=10 кН
Строим эпюру продольных сил
Вычисляем ординаты эпюры нормальных напряжений
σ1 = = = –200МПа
σ2 = = = –150МПа
σ 3=== 50МПа
Строим эпюры нормальных напряжений.
4. Определяем перемещение свободного конца бруса
∆l=∆l1+∆l2+∆l3
∆l1= = = – 0,5мм
∆l2= = = – 0,225мм
∆l3= = = 0,05мм
∆l= — 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
Задача № 2
Из условия прочности определить размеры поперечного сечения стержня, удерживающего в равновесии балку, если предел текучести материала σ т=320МПа, заданный коэффициент запаса прочности [n] = 2,5. Расчет провести для двух случаев:
1. поперечное сечение стержня – круг;
2. поперечное сечение стержня – квадрат.
Вторая задача может быть решена студентами, если они будут ясно представлять смысл условия прочности при растяжении (сжатии).
Последовательность решения задачи:
Балку, равновесие которой рассматривается, освободить от связей и заменить действия связей их реакциями;
Составить уравнение равновесия, причем принять за точку, относительно которой определяются моменты, точку в которой установлена опора, и определяем продольную силу N;
Определить из условия прочности площадь поперечного сечения стержня;
Определить для двух случаев размеры поперечного сечения стержня.
Для круга – диаметр d;
Для квадрата – сторону a.
Решение
Составляем уравнение равновесия и определяем продольную силу N
Σ m A=0
N∙sin30°∙3 – 3q∙1,5 + F∙1 = 0
N= = = 53,3 кН
2. Определяем допускаемое нормальное напряжение
[σ]= | σ | = = 128 МПа |
| [n] |
3. Определяем площадь поперечного сечения стержня
σmax | = | N | ≤ [σ]→A ≥ | N | = | 53,3∙103 | =416 мм2 |
| A | [σ] | 128 |
4. Определяем размеры попе речного сечения круга – диаметр d
А= →d= = = 23 мм
5. Определяем размеры поперечного сечения квадрата – сторону a
A=a2→a= = = 20,4 мм.
IV. Задания для самостоятельного решения
Задача №1
Проверить прочность стальной тяги ВО диаметром d=20мм,если предел текучести σт =240МПа.требуемый коэффициент запаса прочности [n]=1,5
Ответ: перегружена на 58,75%
Задача 2.
Проверить прочность стальных брусьев, если [σ]=160МПа
Ответ: а) перегружен на 4,4%
б) недогружен на 7,5%
Задача 3.
Определить требуемую площадь А поперечного сечения стального бруса, если [σ]=160МПа,
Ответ: а) А=188мм2
б) А=90,6мм2
Задача№4
Определить допускаемую нагрузку для стального стержня, если σт =250МПа, [n]=1,6
Ответ: [F]=31,2кН
Задача №5
Определить размеры поперечного сечения стержня кронштейна, если [σр]=160МПа, [σсж]=120МПа
Ответ: а=10мм,d=10мм.
Практическая работа №9
Источник
