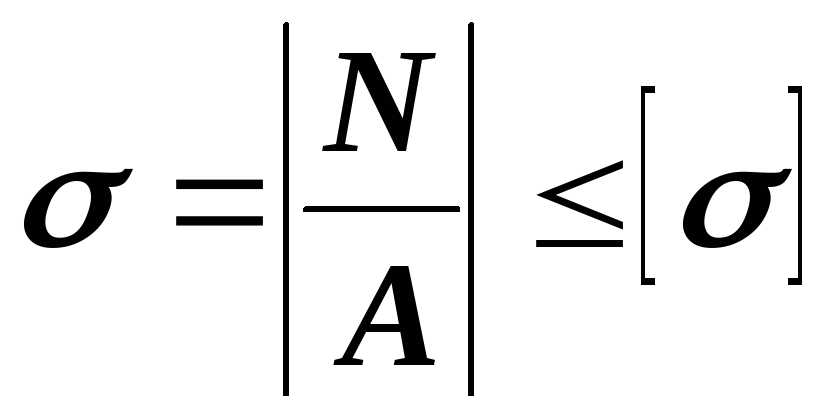Запишите условие прочности для растяжения
Содержание статьи
Растяжение-сжатие.
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии — отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность — свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость — свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость — свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость — свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой — на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Условие прочности при растяжении сжатии
Условие прочности при растяжении (сжатии) выражается неравенством:
где [σ] — допускаемые напряжения, определяются как:
n — коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
38. Допускаемое напряжение
Допускаемое (допустимое) напряжение — это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку.
Допускаемые напряжения либо предписываются компетентной инстанцией, либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции.
39. Закон Гука для сдвига.
Установлено: касательные напряжения пропорциональны углу сдвига в определенных пределах упругой деформации сдвига. Соотношение — формула закона Гука при сдвиге.
Коэффициент пропорциональности G в формуле закона Гука при сдвиге — модуль сдвига. Модуль сдвига измеряется в МПа, кН/см2, кгс/см2, кгс/мм2. Угол сдвига -безразмерная величина.
Модуль сдвига (G) — это физическая постоянная для материала, характеризующая жесткость при сдвиге. Значение модуля сдвига (G) может быть определено экспериментально.
40. Крутящие моменты и их эпюры.
Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов — это график, показывающий изменения крутящего момента по длине вала .
Правило знаков для эпюры крутящих моментов
При построении эпюры крутящих моментов используется правило знаков:
Скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент, направленный по ходу часовой стрелки, противодействуя скручивающему моменту.
41. Условие прочности при кручении
Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение:
Формула служит для проверочного расчета вала на прочность.
Допускается незначительное (до 5 %) превышение расчетного напряжения над допускаемым напряжением .
При проектировочном расчете требуемый полярный момент сопротивленияопределяется по формуле условия прочности при кручении:
.
Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.
Допускаемое напряжение :
для пластичных материалов назначается в зависимости от предела текучести ( ) при кручении (сдвиге):
.
для хрупких материалов назначается в зависимости от предела прочности:
.
42. Понятие о расчете на жесткость при кручении.
Источник
4. Условие прочности при растяжении. Типы задач.
Основная задача сопротивления материалов — обеспечить надежные размеры детали при действии на нее различных нагрузок. Такие размеры можно определить из расчета на прочность. Прочность стержня при осевом растяжении обеспечена, если для каждого его поперечного сечения выполняется условие прочности:
|
 — абсолютное значение продольной силы;
— абсолютное значение продольной силы;  — площадь поперечного сечения;
— площадь поперечного сечения;
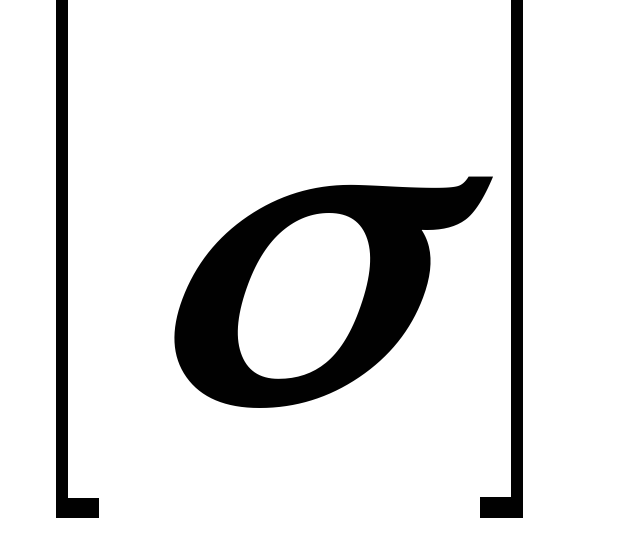 — допускаемое напряжение при растяжении или сжатии для материала стержня.
— допускаемое напряжение при растяжении или сжатии для материала стержня.
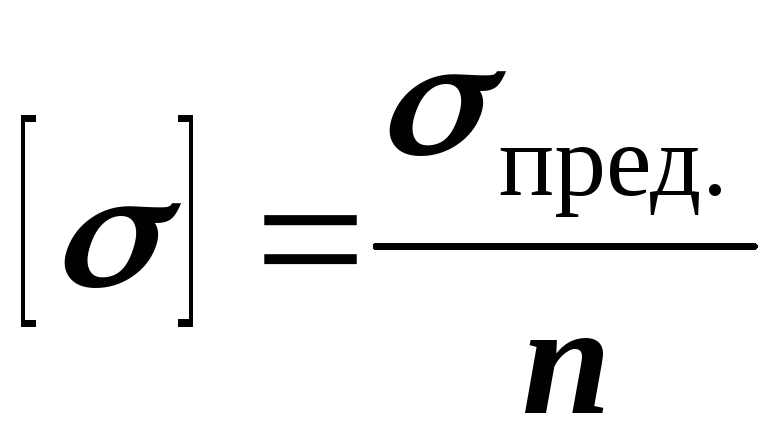 , где
, где  — коэффициент запаса. Для пластичных материалов предельным напряжением является предел текучести
— коэффициент запаса. Для пластичных материалов предельным напряжением является предел текучести , а для хрупких материалов — предел прочности
, а для хрупких материалов — предел прочности .
.
Условие прочности при растяжении или сжатии заключается в том, что наибольшее расчетное напряжение в элементе конструкции не должно превосходить допускаемого напряжения.
С использованием условия прочности выполняются три вида расчетов:
1. Проверочный расчет (проверка прочности). При заданных нагрузках и площади поперечного сечения  определяют расчетное напряжение и сравнивают его с допускаемым
определяют расчетное напряжение и сравнивают его с допускаемым 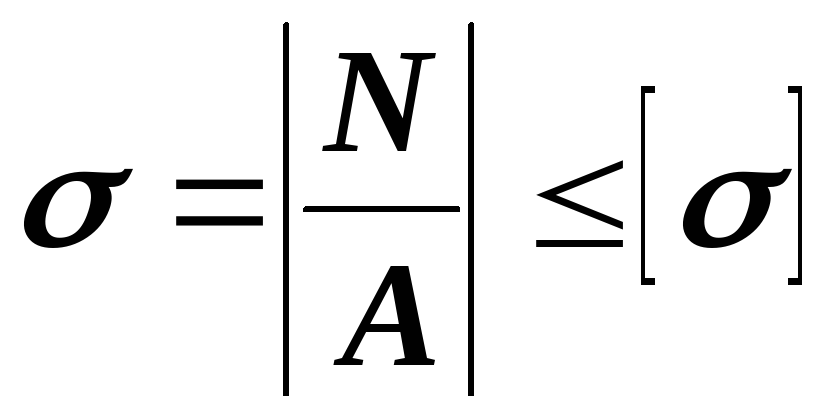 . Превышение расчетного напряжения по сравнению с допускаемым не должно превышать 5 %, иначе прочность рассчитываемой детали считается недостаточной.
. Превышение расчетного напряжения по сравнению с допускаемым не должно превышать 5 %, иначе прочность рассчитываемой детали считается недостаточной.
2. Проектировочный расчет (подбор сечения). По известным нагрузкам и допускаемому напряжению 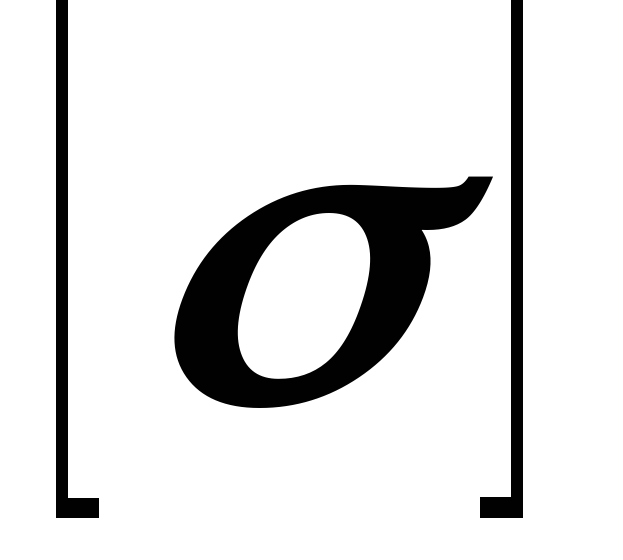 определяют необходимые размеры поперечного сечения
определяют необходимые размеры поперечного сечения
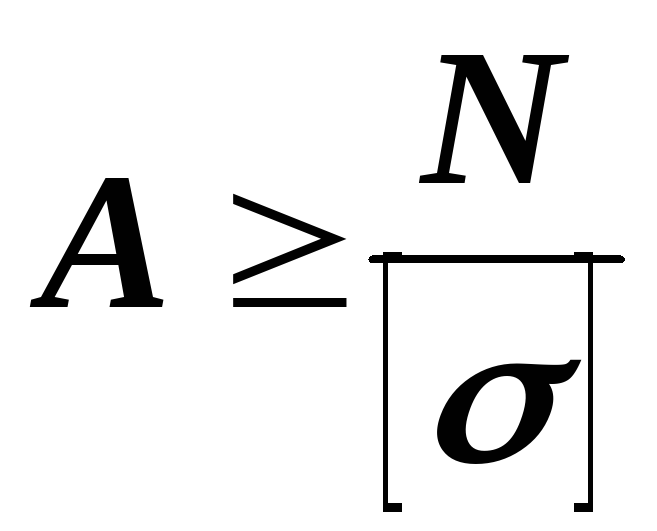 .
.
3. Определение допускаемой нагрузки. По известным размерам и материалу детали определяют допускаемую нагрузку 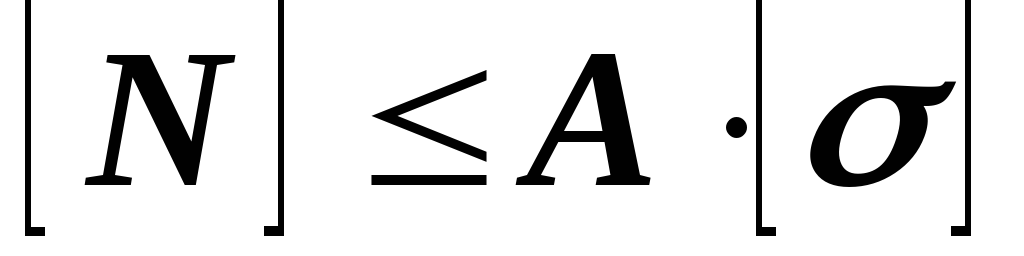 .
.
5. Статически неопределимые конструкции.
Статически неопределимыми называются такие конструкции, в элементах которых при помощи только одних уравнений статики определить усилия невозможно. Кроме уравнений статики для расчета таких конструкций необходимо использовать также уравнения, содержащие деформации элементов конструкций. Эти уравнения называются уравнениями совместности деформаций.
В статически неопределимых конструкциях число неизвестных, подлежащих определению, больше, чем число уравнений статики, которые можно составить для данной системы. Разность между числом неизвестных и числом уравнений статики называется степенью статической неопределимости.
Последовательность расчета статически неопределимых систем рассмотрим на примере:
Задание: Прямой однородный стержень, имеющий постоянную площадь поперечного сечения  , закреплен по концам и нагружен силой
, закреплен по концам и нагружен силой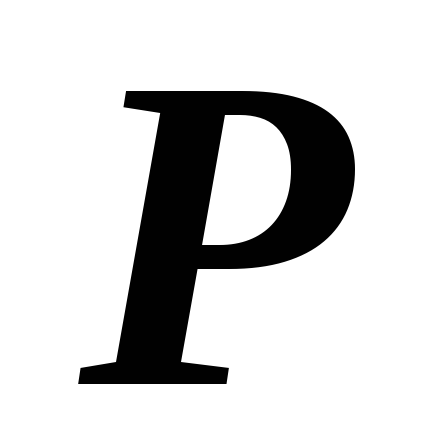 (рис. 36). Построить эпюры продольных сил
(рис. 36). Построить эпюры продольных сил , нормальных напряжений
, нормальных напряжений и продольных перемещений точек — границ участков
и продольных перемещений точек — границ участков . Модуль продольной упругости материала
. Модуль продольной упругости материала .
.
1
Рис. 36.
. Находим степень статической неопределимости:
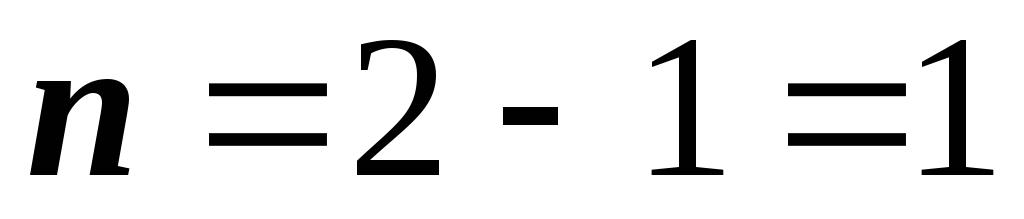 (система один раз статически неопределима).
(система один раз статически неопределима).
2. Составляем уравнение статики: 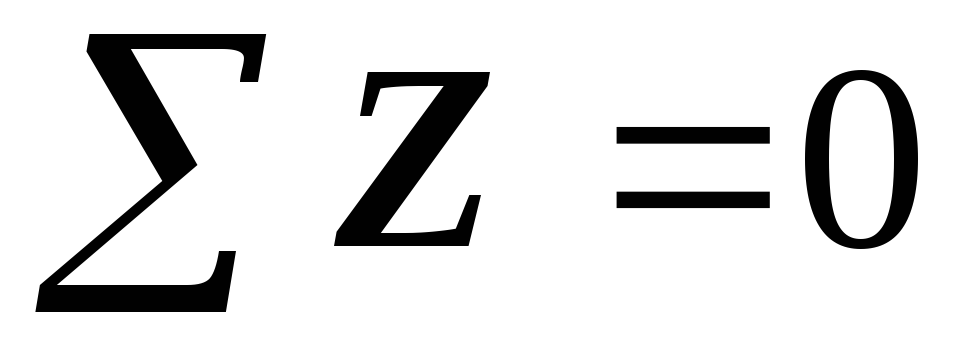 .
.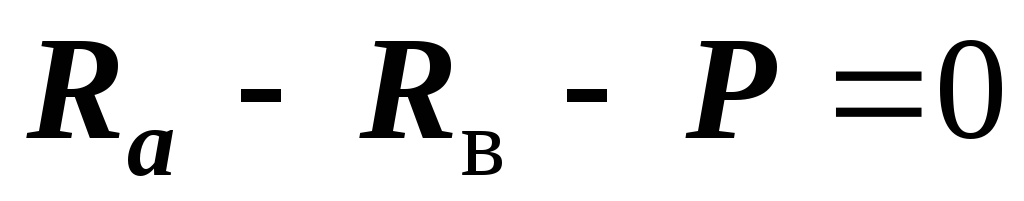 .
.
3. Разбиваем брус на участки. Границами участков являются точки приложения сосредоточенных сил, сечения, в которых изменяется площадь.
4. С использованием метода сечений выражаем продольные силы на участках через одну опорную реакцию.
1 — й участок: 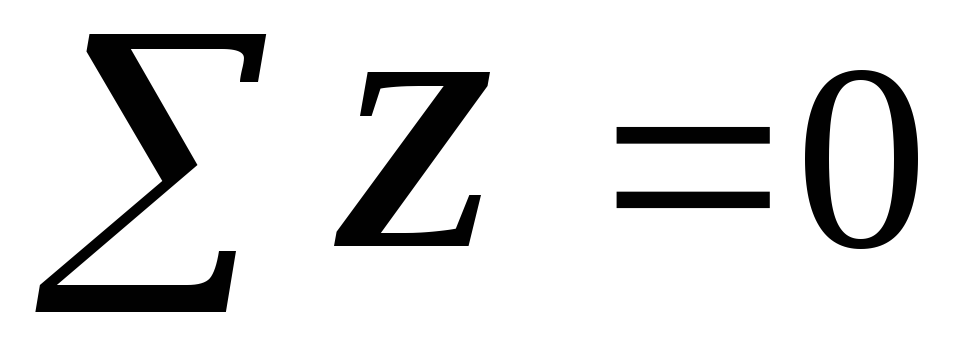 .
.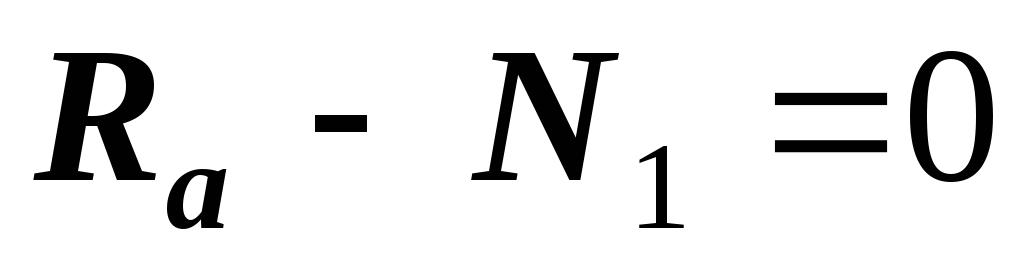 .
.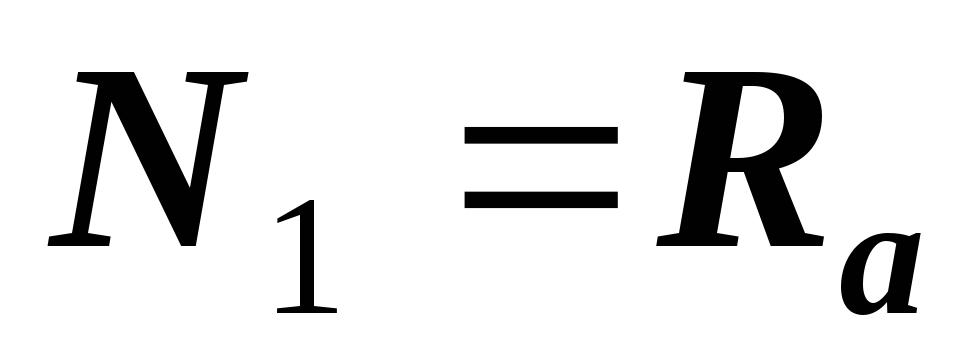 ;
;
2 — й участок: 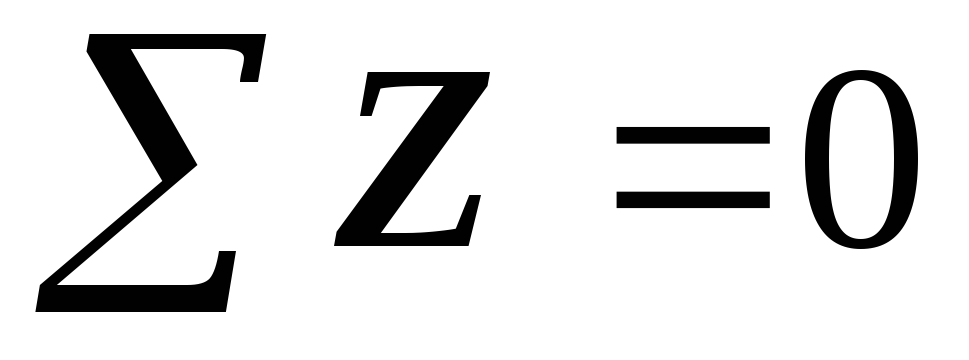 .
.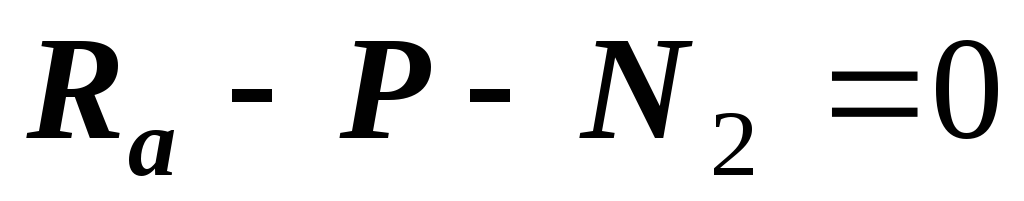 .
.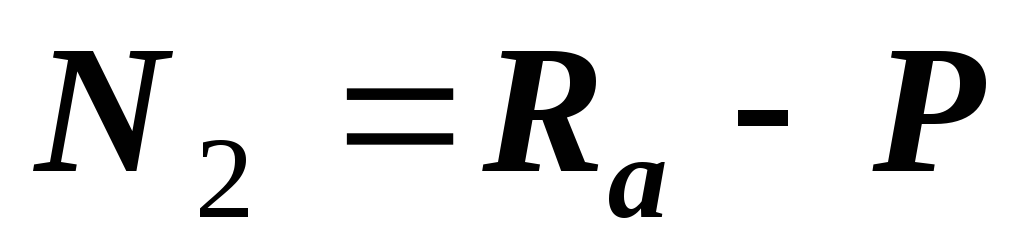 .
.
5. Составляем уравнение совместности деформаций участков бруса. Так как концы бруса жестко защемлены, то его общая длина не изменяется, т.е.
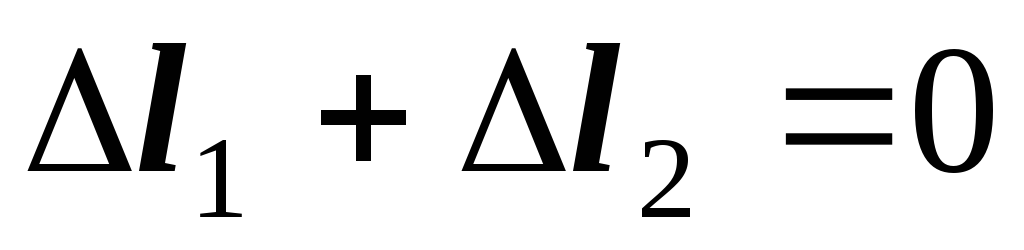 .
.
6. Записываем выражения закона Гука, выражая абсолютные деформации участков через усилия, возникающие в поперечных сечениях
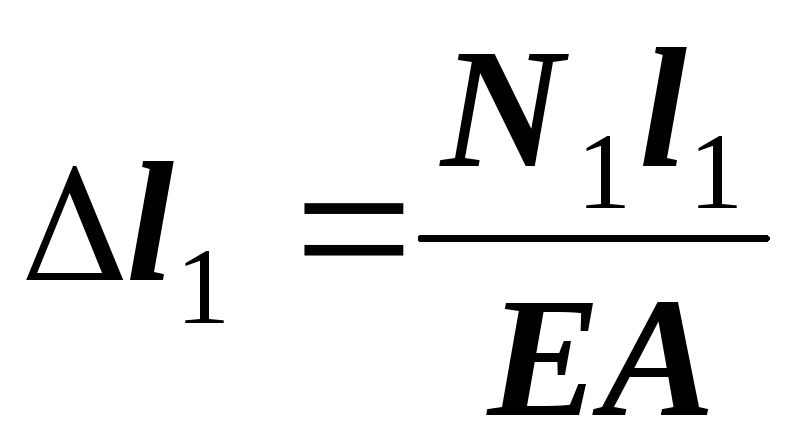
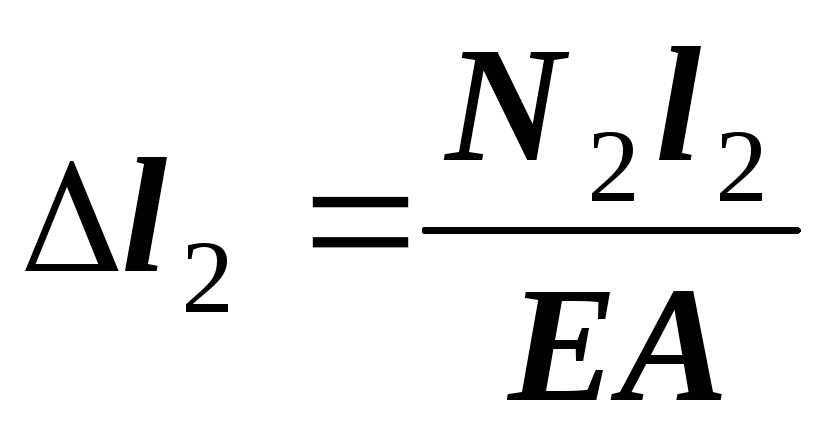 .
.
7. Подставляем выражения закона Гука в уравнение совместности деформаций
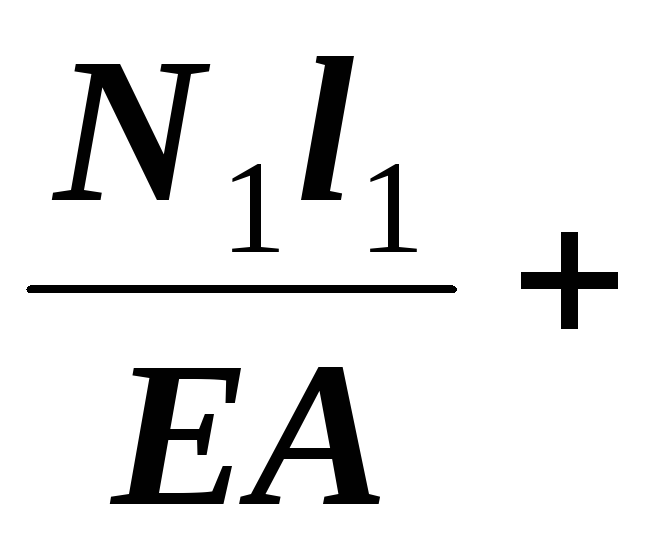
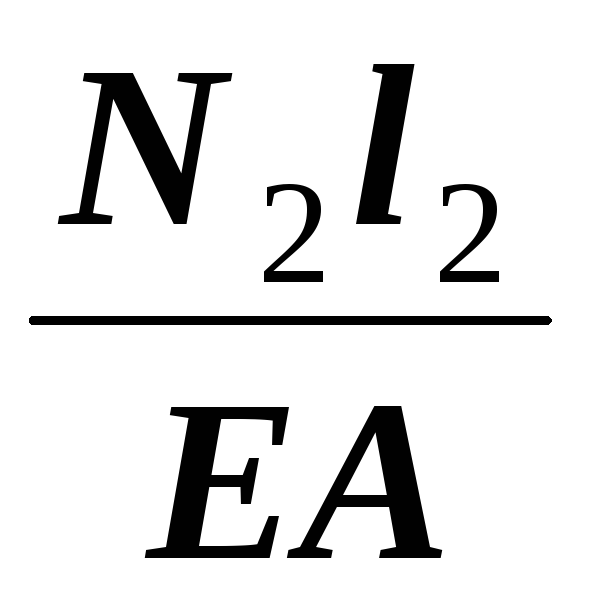 = 0.
= 0.
Отсюда 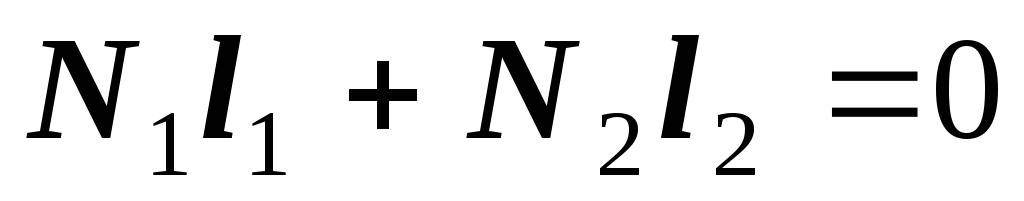 ;
;
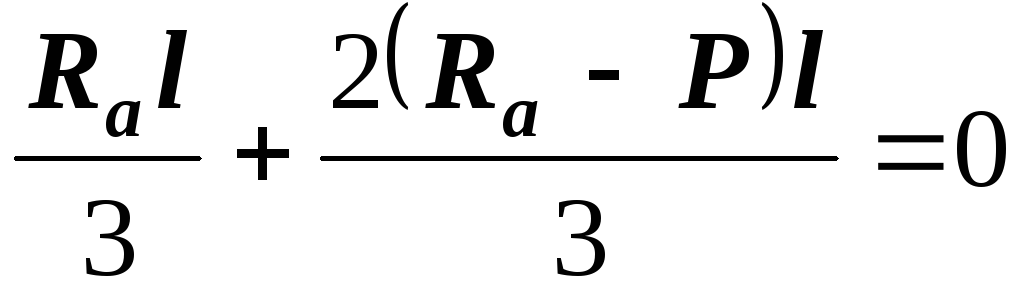 ;
; 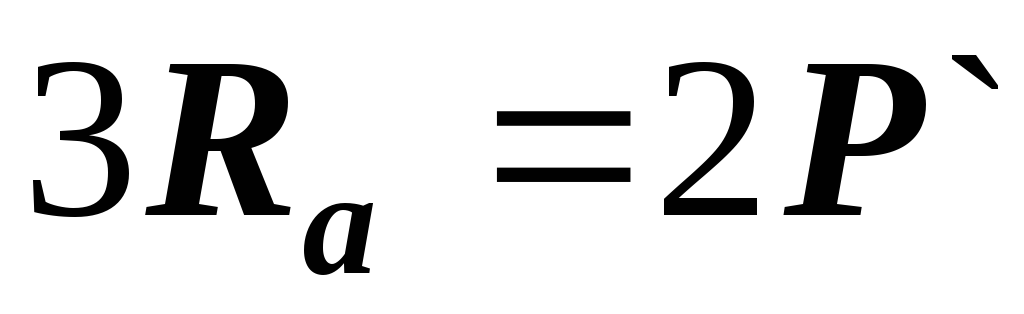 ;
;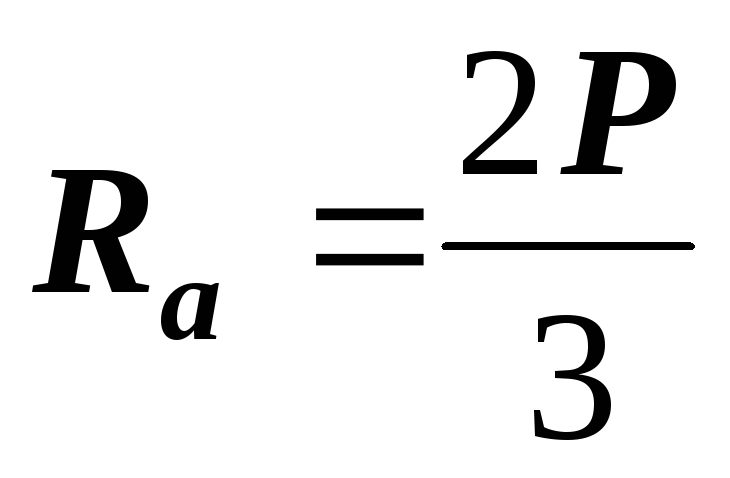 .
.
8. Определяем продольные силы на участках и строим эпюру  .
.
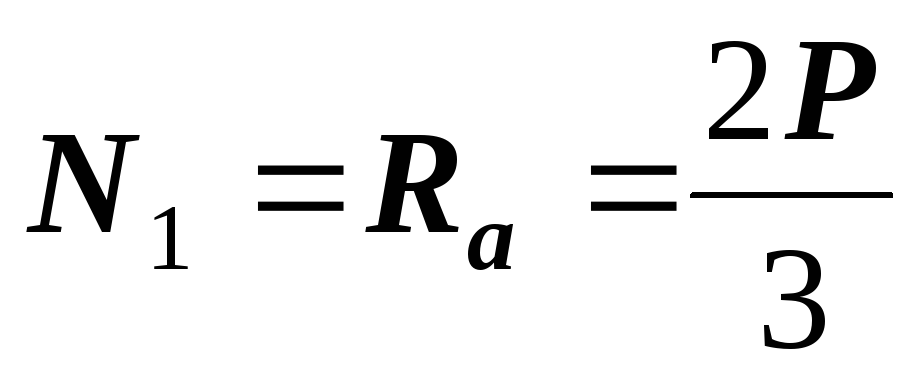 (растяжение);
(растяжение); 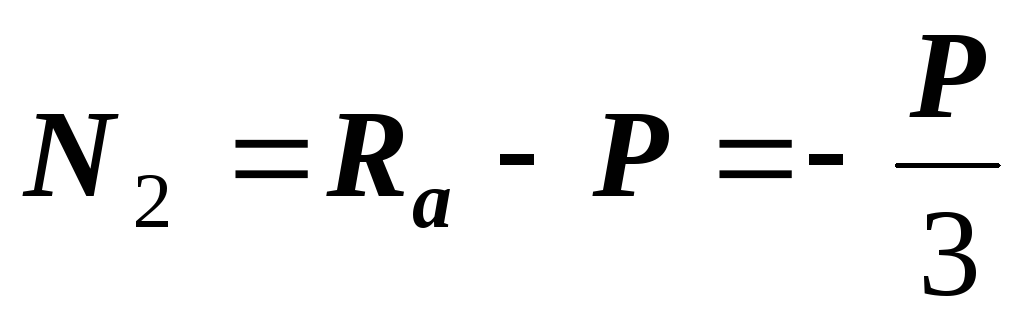 (сжатие).
(сжатие).
9. Определяем нормальные напряжения и строим эпюру .
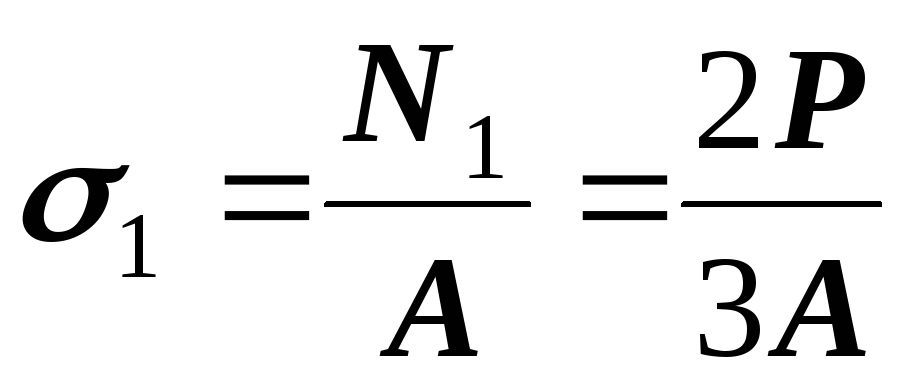 (растяжение);
(растяжение); 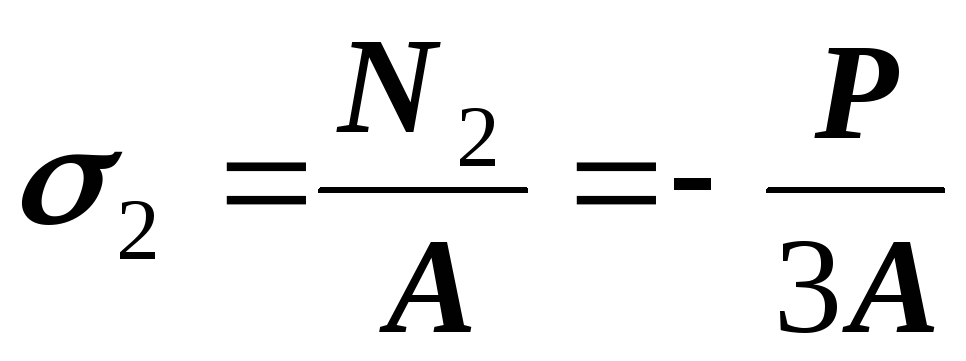 (сжатие).
(сжатие).
10. Определяем перемещения точек — границ участков и строим эпюру  . Для этого определяем абсолютные деформации участков по закону Гука.
. Для этого определяем абсолютные деформации участков по закону Гука.
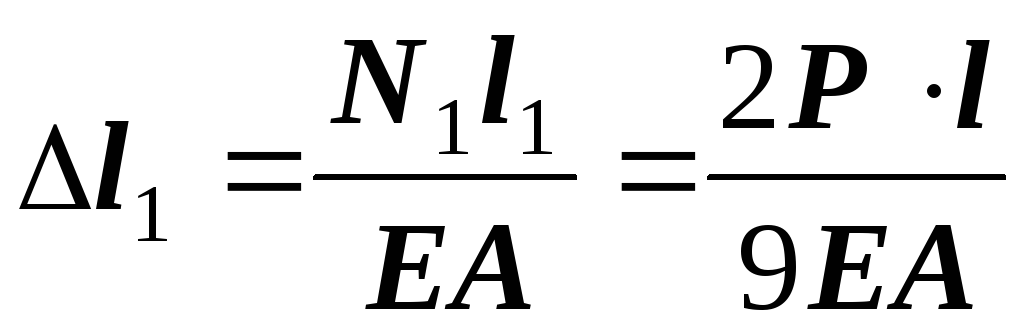 ;
; 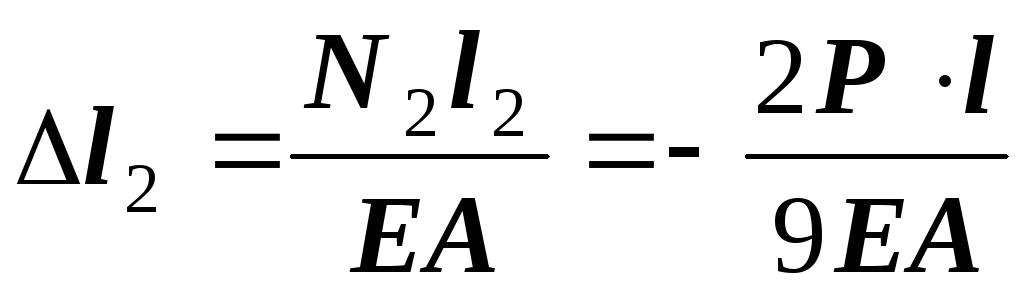 .
.
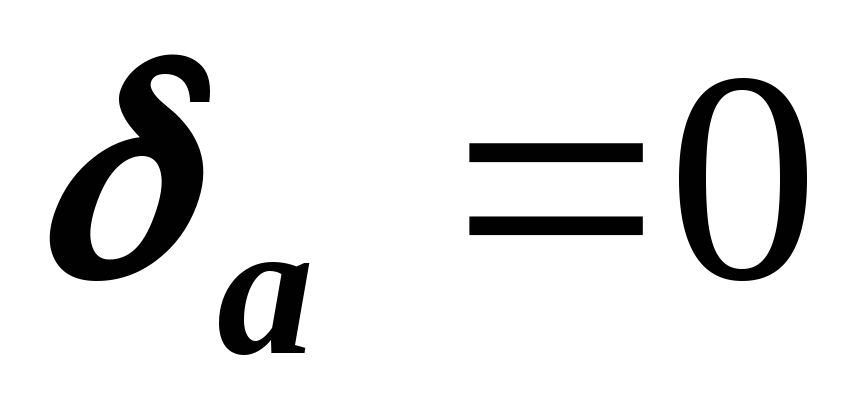 ;
; 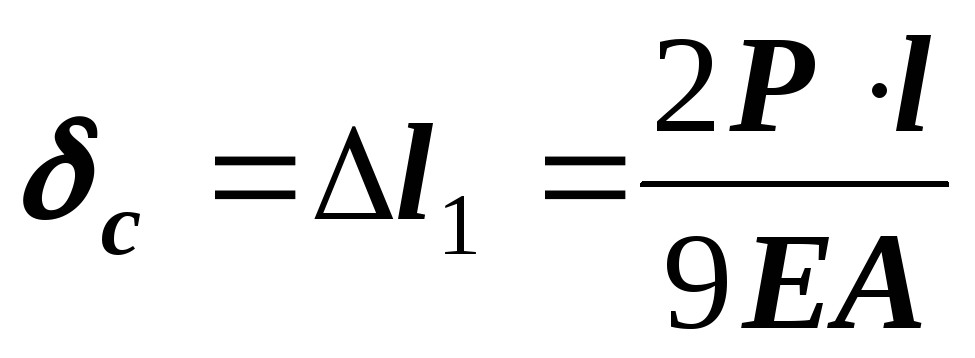 ;
;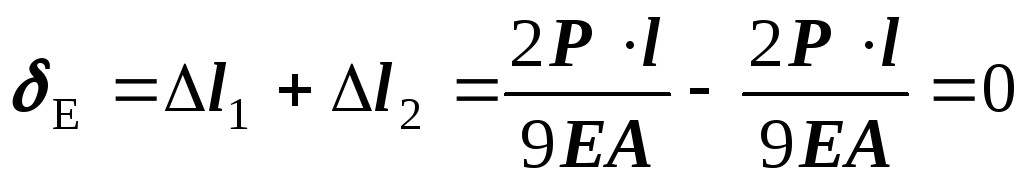 .
.
Источник
Основное условие прочности. допускаемые напряжения. условие жесткости
| ОСНОВНОЕ УСЛОВИЕ ПРОЧНОСТИ. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. УСЛОВИЕ ЖЕСТКОСТИ |
| Ответы на вопросы о прочности может дать оценка прочности конструкции, которая сводится к сравнению расчетных напряжений с допускаемыми: |
| Это и есть основные условия прочности. |
| Расчетное напряжение — наибольшее по абсолютной величине сжимающее или стягивающее напряжение, возникающее в опасном сечении конструкции. |
| Допускаемые напряжения. |
| Допускаемое напряжение определяется по формуле: |
| Механические характеристики материалов — величины предела текучести и предела прочности определяются опытным путем. Автоматически вычерчивается график «сила — продольная деформация» (Р -l) Этот график переводится в диаграмму напряжение — относительная деформация . |
| где . (Здесь F0 и l0 — первоначальная площадь поперечного сечения и длина стандартного образца) (рис. 1.22). |
| Рис. 1.22 |
| — предел пропорциональности; наибольшее напряжение, при котором еще справедлив закон Гука; |
| — предеп текучести (деформации растут без увеличения нагрузки); |
| Рис. 1.23 |
| — предел прочности ипи временное сопротивпение разрыву (рис.1 23). |
| — предел прочности при растяжении, |
| — предеп прочности при сжатии, причем: |
| В спучае пластичного материапа в качестве предельного напряжения |
| — принимается предеп текучести при растяжении , соответствующий началу текучести материала, а в случае хрупкого материала — предел прочности при растяжении или сжатии, предшествующий разрыву образца. |
| В знаменателе стоит нормативный (требуемый) коэффициент запаса прочности по отношению соответственно к пределу текучести и пределу прочности n. |
| Он представляет собой величину, большую единицы, зависящую от класса конструкции (капитальная, временная и т.п.), срока ее эксплуатации, нагрузки (статическая, циклическая и т.п.), возможной неоднородности изготовления материала и от вида деформации (растяжение, сжатие, изгиб и т.п.). |
| Нормативный коэффициент запаса прочности регламентируется для строительных конструкций СН и Пами, для машиностроительных — внутризаводскими нормами. В большинстве случаев он принимается равным для пластичных материалов nT = 1,5 + 2,5, для хрупких nB = 2,5 + 5. |
| В случае, когда решающими для прочности конструкции являются не нормальные, а касательные напряжения (например, при кручении бруса круглого поперечного сечения), условие прочности имеет вид: |
| — расчетное касательное напряжение. |
| — допускаемое касательное напряжение, определяемое по формуле: |
| В случае пластичного материала в качестве предельного принимают предел текучести при сдвиге в случае хрупкого материала — предел прочности . |
| В большинстве случаев допускаемые напряжения при кручении принимают в зависимости от допускаемых напряжений при растяжении того же материала. Например, для стали = 0,5 [], для чугуна . |
| В практике инженерных расчетов считают возможным допускать перенапряжение материала до 3 — 5%. |
| Условие жесткости по логике строится так же, как и условие прочности. Однако, ограничения накладываются не на напряжения, а на изменение формы стержня (вала, балки), т.е. деформации. Для разных видов нагружения условия жесткости имеютвид: при растяжении (сжатии) |
| при кручении |
| где — угол закручивания, |
| при изгибе |
| где — угол поворота, у — прогиб. |
Источник